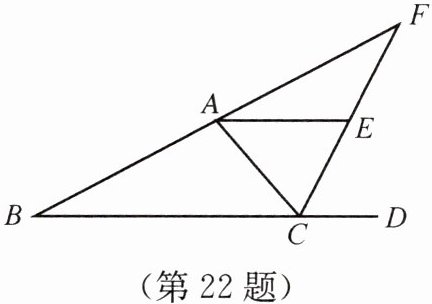
22. 如图,$\triangle ABC的外角\angle ACD的平分线与线段BA的延长线交于点F$,点$E在线段CF$上,且$\angle AEF+\angle FCD= 180^\circ$.
(1)判断$AE$,$BC$是否平行,并说明理由;
(2)若$\angle B= 28^\circ$,$\angle ACF= 62^\circ$,求$\angle BAC$的度数.
答案:
(1) 因为$∠AEF+∠AEC=180^{\circ},∠AEF+∠FCD=180^{\circ}$,所以$∠AEC=∠FCD$,所以$AE// BC$
(2) 因为CF是$∠ACD$的平分线,$∠ACF=62^{\circ},∠B=28^{\circ}$,所以$∠ACD=2∠ACF=124^{\circ}$,所以$∠BAC=∠ACD - ∠B=124^{\circ}-28^{\circ}=96^{\circ}$
23. 将从1开始的连续自然数按如图所示的方式排列:规定位于第$m$行,第$n$列的自然数10记为(3,2),自然数15记为(4,2)……按此规律,回答下列问题:
(1)(6,3)表示的自然数是______
22
.
(2)自然数2018记为______
(505,2)
.
(3)用一个正方形方框在第3列和第4列中任意框四个数,这四个数的和能为2018吗?如果能,求出框出的四个数中最小的数;如果不能,请写出理由.
若正方形框内第一行为奇数行,设框出的四个数中最小的数为x,则另外三个数分别为$x + 1,x + 2,x + 3$,根据题意,得$x + x + 1 + x + 2 + x + 3 = 2018$,解得$x = 503$,因为$503 = 4×125 + 3$,所以503为第126行的自然数,不符合题意,舍去;若正方形框内第一行为偶数行,设框出的四个数中最小的数为y,则另外三个数分别为$y + 1,y + 6,y + 7$,根据题意,得$y + y + 1 + y + 6 + y + 7 = 2018$,解得$y = 501$,因为$501 = 4×125 + 1$,所以501为第126行第4列的自然数,符合题意,所以这四个数的和能为2018,框出的四个数中最小的数为501
答案:
(1) 22
(2) (505,2)
(3) 若正方形框内第一行为奇数行,设框出的四个数中最小的数为x,则另外三个数分别为$x + 1,x + 2,x + 3$,根据题意,得$x + x + 1 + x + 2 + x + 3 = 2018$,解得$x = 503$,因为$503 = 4×125 + 3$,所以503为第126行的自然数,不符合题意,舍去;若正方形框内第一行为偶数行,设框出的四个数中最小的数为y,则另外三个数分别为$y + 1,y + 6,y + 7$,根据题意,得$y + y + 1 + y + 6 + y + 7 = 2018$,解得$y = 501$,因为$501 = 4×125 + 1$,所以501为第126行第4列的自然数,符合题意,所以这四个数的和能为2018,框出的四个数中最小的数为501