10. 一列火车匀速行驶,经过一条长600m的隧道需要45s的时间,隧道顶部有一盏固定的灯,若该灯在火车上垂直照射了15s,则火车的长为
300
m.
答案:300
解析:
设火车的长为$x$米,火车的速度为$v$米/秒。
因为灯在火车上垂直照射了15秒,所以火车通过灯光时行驶的路程为火车自身长度$x$,则$v = \frac{x}{15}$。
火车经过长600米的隧道需要45秒,此时行驶的路程为火车长加隧道长,即$x + 600$,则$v = \frac{x + 600}{45}$。
所以$\frac{x}{15} = \frac{x + 600}{45}$,
两边同乘45得:$3x = x + 600$,
$3x - x = 600$,
$2x = 600$,
$x = 300$。
300
11. 甲、乙两人年龄不同,已知当甲与乙现在的年龄相同时,乙6岁;当乙与甲现在的年龄相同时,甲21岁.今年甲的年龄是
16
岁.
答案:16
解析:
设甲今年的年龄为$x$岁,乙今年的年龄为$y$岁,年龄差为$d$岁,则$d = x - y$。
当甲与乙现在的年龄相同时,即甲$y$岁时,乙的年龄为$y - d = 6$,可得$y - (x - y) = 6$,化简为$2y - x = 6$。
当乙与甲现在的年龄相同时,即乙$x$岁时,甲的年龄为$x + d = 21$,可得$x + (x - y) = 21$,化简为$2x - y = 21$。
联立方程组$\begin{cases}2y - x = 6 \\ 2x - y = 21\end{cases}$,解得$x = 16$。
16
12. 定义新运算“*”:$x*y = x + y - xy$,如$2*(-3)= 2 + (-3)-2×(-3)= 5$,那么当$[(-x)*(-2)]*2 = 2x$时,$x= $
-4
.
答案:-4
解析:
先计算$(-x)*(-2)$:
$(-x)*(-2)=(-x)+(-2)-(-x)×(-2)=-x - 2 - 2x=-3x - 2$
再计算$(-3x - 2)*2$:
$(-3x - 2)*2=(-3x - 2)+2 - (-3x - 2)×2=-3x - 2 + 2 + 6x + 4=3x + 4$
由$[(-x)*(-2)]*2 = 2x$,得$3x + 4 = 2x$,解得$x=-4$
$-4$
13. 年底促销,某商场促销活动如下表:
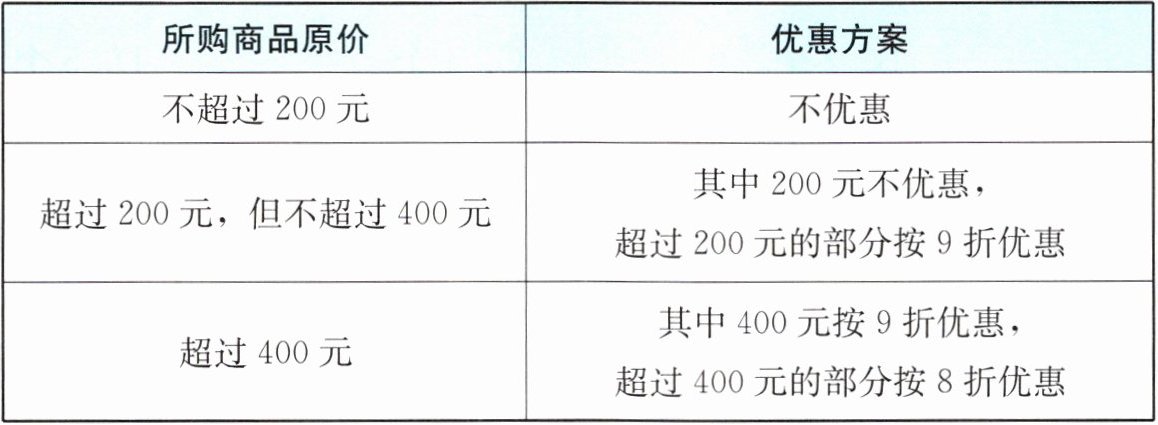
小北和小明均在该商场购买了商品,其中小北实际付款218元,小明实际付款362元,则他们两人购买的商品原价之和是______元.
600或622.5
答案:600或622.5
解析:
设小北购买商品的原价为$x$元,小明购买商品的原价为$y$元。
小北:
若$x \leq 200$,付款$x = 218$,矛盾,舍去。
若$200 < x \leq 400$,付款$200 + 0.9(x - 200) = 218$,解得$x = 220$。
小明:
若$200 < y \leq 400$,付款$200 + 0.9(y - 200) = 362$,解得$y = 380$,此时原价之和$220 + 380 = 600$。
若$y > 400$,付款$400 × 0.9 + 0.8(y - 400) = 362$,解得$y = 402.5$,此时原价之和$220 + 402.5 = 622.5$。
600或622.5
14. 解方程:
(1)$5x + 2 = -8$;
(2)$3x - 4(2x + 5)= x + 4$;
(3)$\frac{x - 1}{3}-\frac{x + 2}{6}= \frac{4 - x}{2}$;
(4)$\frac{x - 2}{0.2}-\frac{x + 1}{0.3}= 1$.
答案:(1)$x=-2$;(2)$x=-4$;(3)$x=4$;(4)$x=8.6$
解析:
(1)解:$5x=-8-2$
$5x=-10$
$x=-2$
(2)解:$3x-8x-20=x+4$
$3x-8x-x=4+20$
$-6x=24$
$x=-4$
(3)解:$2(x-1)-(x+2)=3(4-x)$
$2x-2-x-2=12-3x$
$2x-x+3x=12+2+2$
$4x=16$
$x=4$
(4)解:$\frac{10(x-2)}{2}-\frac{10(x+1)}{3}=1$
$5(x-2)-\frac{10(x+1)}{3}=1$
$15(x-2)-10(x+1)=3$
$15x-30-10x-10=3$
$5x=43$
$x=\frac{43}{5}=8.6$
15. 已知$M$,$N$代表两个整式,其中$M = 2a^2 - 3$,$N与M的和为5a^2 + 2a$.
(1)求整式$N$;
(2)若$a是方程2(x - 1)+3 = x$的解,求整式$N$的值.
答案:(1)$N=(5a^{2}+2a)-(2a^{2}-3)=5a^{2}+2a-2a^{2}+3=3a^{2}+2a+3$;(2)由$2(x-1)+3=x$得,$2x-2+3=x$,$x=-1$,因为a是方程$2(x-1)+3=x$的解,所以$a=-1$。所以$3a^{2}+2a+3=4$
解析:
(1) $ N=(5a^{2}+2a)-(2a^{2}-3) $
$=5a^{2}+2a-2a^{2}+3 $
$=3a^{2}+2a+3$
(2) 解方程$2(x - 1)+3 = x$:
$2x - 2 + 3 = x$
$2x + 1 = x$
$2x - x = -1$
$x = -1$
因为$a$是方程的解,所以$a=-1$。
将$a=-1$代入$N=3a^{2}+2a+3$:
$3×(-1)^{2}+2×(-1)+3$
$=3×1 - 2 + 3$
$=3 - 2 + 3$
$=4$