7. 如图所示是人们用木棒撬石块的示意图。撬石块有两种方法:第一种是以B为支点,在点C用与棒垂直的力$F_1$向下撬;第二种是以A为支点,在点C用与棒垂直的力$F_2$向上撬。(木棒自重不计)
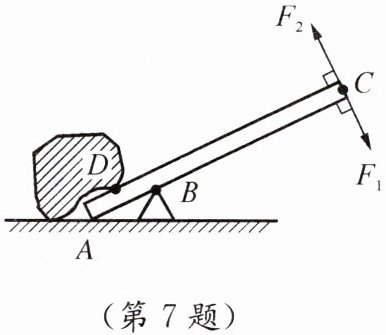
(1)在图中画出力$F_1$的力臂。
(2)如果石块压在棒上的D点正好是AB的中点,你认为第______种方法更省力,理由是______。
答案:(1)如图所示
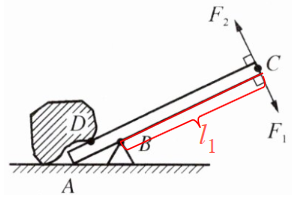
(2)二;第二种方法与第一种方法相比,阻力臂相同,但动力臂更长,所以更省力。
8. 如图所示是互成90°角、重力可忽略不计的硬棒,以O为支点,在点B悬挂重为50 N的重物。若要使硬棒在图示的位置平衡,试画出作用在点A的最小力的方向并计算出该力的大小。

最小力大小为40 N,方向垂直OA向上。
答案:解:由杠杆平衡条件 $F_1l_1 = F_2l_2$ 可知,在阻力和阻力臂一定时,动力臂越长,动力越小。
OB为阻力臂,$l_2 = 4\ \text{cm}$,阻力 $F_2 = 50\ \text{N}$。
OA为最长动力臂,根据勾股定理,$OA = \sqrt{(3\ \text{cm})^2 + (4\ \text{cm})^2} = 5\ \text{cm}$。
则最小动力 $F_1 = \frac{F_2l_2}{l_1} = \frac{50\ \text{N} × 4\ \text{cm}}{5\ \text{cm}} = 40\ \text{N}$。
力的方向垂直于OA向上。
答案:最小力大小为40 N,方向垂直OA向上。
9. 一杠杆经调节后在水平位置平衡。如图所示,在点A悬挂3个钩码(每个钩码重0.5 N),要使杠杆在水平位置平衡,需在点B悬挂
2
个钩码。取走悬挂在点B的钩码,改用弹簧测力计在点C竖直向上拉,使杠杆在水平位置平衡,弹簧测力计的拉力为
3
N。若改变弹簧测力计拉的方向,使之斜向右上方,杠杆仍然在水平位置平衡,则弹簧测力计的示数将
变大
。

答案:解:设每个小格长度为L。
点A悬挂3个钩码,每个钩码重0.5N,所以$F_A=3×0.5N=1.5N$,$L_A=2L$。
点B到O的距离$L_B=3L$,设点B悬挂n个钩码,$F_B=n×0.5N$。
由杠杆平衡条件$F_A× L_A=F_B× L_B$得:$1.5N×2L=0.5N× n×3L$,解得$n=2$。
取走B点钩码,在C点竖直向上拉,$L_C=1L$,设拉力为F。
由杠杆平衡条件$F_A× L_A=F× L_C$得:$1.5N×2L=F×1L$,解得$F=3N$。
改变弹簧测力计方向斜向右上方,拉力力臂变小,阻力和阻力臂不变,由杠杆平衡条件可知,拉力变大,即弹簧测力计示数将变大。
2;3;变大