5. 如图所示是小华制作的斜拉桥模型,她用长30 cm、重5 N的质地均匀的木条OA做桥面,立柱GH做桥塔。OA可绕点O转动,A端用细线与GH上的点B相连,桥面OA实质是一种
杠杆
(填简单机械名称)。保持桥面水平,细线对OA的拉力F=
5
N;将细线一端的固定点由点B改至点C,拉力F的大小变化情况是
变小
,由此小华初步了解到建造高桥塔的好处。
答案:1. 首先判断简单机械名称:
由图可知,$OA$可绕点$O$转动,所以桥面$OA$实质是一种杠杆。
2. 然后计算拉力$F$:
已知木条$OA$长$L = 30cm$,质地均匀,其重心在中点,所以阻力臂$l_{2}=\frac{OA}{2}=\frac{30cm}{2}=15cm$。
由图可知,拉力$F$的力臂$l_{1}=\frac{OA}{2}=\frac{30cm}{2}=15cm$(因为$\angle AOB = 30^{\circ}$,根据直角三角形中$30^{\circ}$所对直角边是斜边的一半,力臂$l_{1}=\frac{OA}{2}$)。
根据杠杆平衡条件$F_{1}l_{1}=F_{2}l_{2}$,这里$F_{2}=G = 5N$,$l_{1}=15cm$,$l_{2}=15cm$,则$F× l_{1}=G× l_{2}$,即$F×15cm = 5N×15cm$,解得$F = 5N$。
3. 最后分析拉力$F$的大小变化情况:
将细线一端的固定点由点$B$改至点$C$,阻力$G$和阻力臂$l_{2}$不变,拉力的力臂$l_{1}$变大。
根据杠杆平衡条件$F_{1}l_{1}=F_{2}l_{2}$($F_{2}l_{2}$不变,$l_{1}$变大),所以拉力$F$变小。
故答案依次为:杠杆;$5$;变小。
6. 根据要求作图:
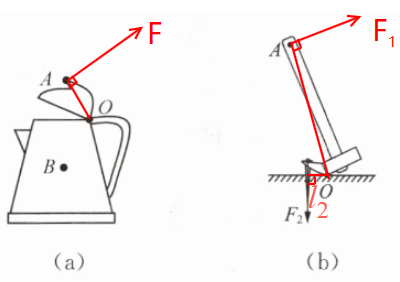
(1)图(a)所示的是一个电热水壶的示意图,B为重心,用力作用在壶盖上点A时,可将壶盖打开。请在点A画出开盖所需最小的力F的示意图(O为支点)。
(2)如图(b)所示,利用羊角锤撬钉子,请你在羊角锤的点A处画出所能施加的最小动力$F_1,$并画出阻力$F_2$的阻力臂$l_2。$
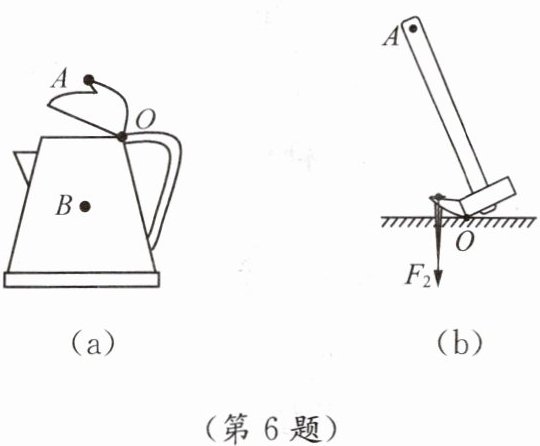
答案: