1. 甲、乙两台抽水机的功率分别为 500 W 和800 W。下列说法正确的是(
D
)。
A.抽水机甲做功少
B.抽水机乙做功多
C.抽水机甲做功快
D.抽水机乙做功快
答案:【解析】:
本题主要考查对功率概念的理解。功率是描述做功快慢的物理量,它表示单位时间内完成的功。功率的计算公式为$P = \frac{W}{t}$,其中$P$是功率,$W$是功,$t$是时间。从这个公式可以看出,功率大意味着在相同时间内完成的功多,或者说完成相同的功所需的时间少。
对于选项A和B,它们涉及到的是做功的多少,而功率本身并不直接决定做功的多少,而是决定做功的快慢。因此,不能仅凭功率的大小来判断做功的多少,还需要考虑时间因素。所以A和B选项都是错误的。
对于选项C和D,它们涉及到的是做功的快慢,这正是功率所描述的。由于题目中给出乙抽水机的功率大于甲抽水机的功率,因此乙抽水机做功更快。所以C选项错误,D选项正确。
【答案】:
D.抽水机乙做功快。
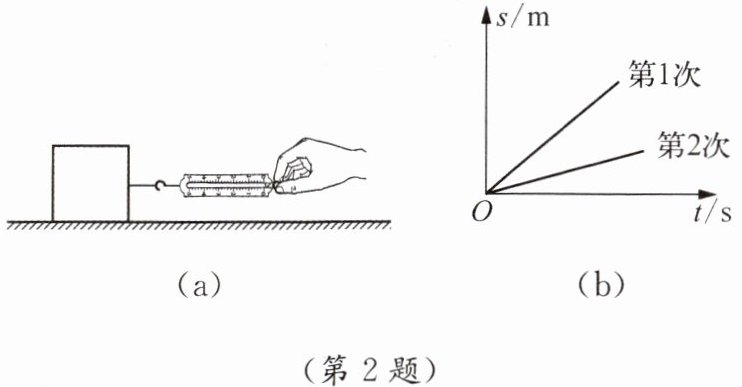
2. 如图(a)所示,木块放在水平面上,用弹簧测力计沿水平方向拉木块做直线运动,两次拉动木块得到的s-t图像如图(b)所示。两次对应的弹簧测力计示数分别为$F_1、$$F_2,$两次拉力的功率分别为$P_1、$$P_2,$下列判断正确的是(
B
)。
$A. F_1>F_2、$$P_1>P_2$
$B. F_1= F_2、$$P_1>P_2$
$C. F_1>F_2、$$P_1= P_2$
$D. F_1<F_2、$$P_1<P_2$
答案:解:
1. 由图(b)可知,两次拉动木块均做匀速直线运动,故拉力等于滑动摩擦力。
2. 木块对水平面的压力和接触面粗糙程度不变,滑动摩擦力不变,因此 $F_1 = F_2$。
3. 由 $s-t$ 图像斜率可知,第1次速度 $v_1 >$ 第2次速度 $v_2$。
4. 根据功率公式 $P = Fv$,因 $F_1 = F_2$ 且 $v_1 > v_2$,故 $P_1 > P_2$。
结论:B. $F_1 = F_2$、$P_1 > P_2$
3. 如图所示,分别用定滑轮、动滑轮把重力相等的甲、乙两物体在相同时间内匀速提升相同高度(不计机械自重和摩擦),所用的拉力Fₐ
>
Fᵦ,拉力做功的功率Pₐ
=
Pᵦ。

答案:【解析】:
本题主要考查定滑轮和动滑轮的工作特点以及功率的计算。
首先,分析定滑轮和动滑轮的工作特点。
定滑轮的工作特点是不省力,但可以改变力的方向。因此,使用定滑轮拉甲物体时,拉力$F_a$等于甲物体的重力$G$,即$F_a=G$。
动滑轮的工作特点是能省一半力,但费距离。使用动滑轮拉乙物体时,由于不计机械自重和摩擦,拉力$F_b$是乙物体重力$G$的一半,即$F_b=\frac{1}{2}G$。
由于甲、乙两物体的重力相等,所以可以得出$F_a>F_b$。
接着,分析拉力做功的功率。
功率是表示做功快慢的物理量,计算公式为$P=\frac{W}{t}$,其中$W$是功,$t$是时间。
由于不计机械自重和摩擦,所以拉力做的功等于物体重力做的功,即$W=Gh$。因为甲、乙两物体的重力相等,且在相同时间内匀速提升相同高度,所以拉力做的功也相等,即$W_a=W_b$。
又因为时间相同,所以根据功率的计算公式可以得出$P_a=P_b$。
【答案】:
$>$ ;$=$