7. 如图(a)所示,用弹簧测力计竖直向上缓慢提升静止在水平桌面上的钩码,弹簧测力计的示数F与弹簧测力计的“0”刻度线上升高度h之间的关系如图(b)所示,则钩码的重力大小为
2
N。当弹簧测力计的示数是1.5 N时,钩码受到的合力大小是
0
N。从开始提升到h= 30 cm的过程中,弹簧测力计的拉力对钩码做功为
0.4
J。
答案:【解析】:
本题主要考查了弹簧测力计的读数、力的合成以及功的计算。
从图(b)中可以看出,当$h$在$10cm$到$30cm$之间时,弹簧测力计的示数$F$稳定在$2N$,说明此时钩码处于静止或匀速直线运动状态,受力平衡,钩码的重力$G$等于此时弹簧测力计的示数,即$G=F=2N$。
当弹簧测力计的示数是$1.5N$时,钩码受到竖直向上的拉力$F_{拉}=1.5N$,竖直向下的重力$G=2N$,因为$F_{拉}<G$,钩码仍处于静止状态,所以钩码受到的合力大小$F_{合}=G-F_{拉}=2N-1.5N=0.5N$。
从开始提升到$h=30cm$的过程中,弹簧测力计的拉力对钩码做功分为两个阶段:
第一阶段:$0$到$10cm$,钩码没有被提起,拉力不做功,$W_{1}=0J$。
第二阶段:$10cm$到$30cm$,拉力$F=2N$,移动距离$s=30cm-10cm=20cm=0.2m$,根据功的计算公式$W=Fs$,可得$W_{2}=2N×0.2m=0.4J$。
则弹簧测力计的拉力对钩码做功$W=W_{1}+W_{2}=0J+0.4J=0.4J$。
【答案】:
$2$;$0$;$0.4$
8. 某人用如图所示的健身器材进行锻炼,配重由若干金属块(每块质量为10 kg)组成,锻炼时可以根据自己的实际情况选择金属块的数量。(杆重、绳重及摩擦均不计,g取10 N/kg)
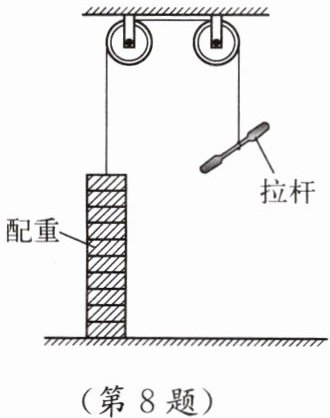
(1)健身器材上的滑轮均属于
定
(定/动)滑轮。
(2)若某人的质量为85 kg,则他一次最多能拉起
8
块金属块。
(3)当他选择6块金属块时,若将拉杆向下拉动0.5 m,则拉力做了多少功?
300J
答案:【解析】:
本题主要考查了定滑轮的特点、重力公式和功的公式的应用。
(1)健身器材上的滑轮在使用过程中,其轴的位置固定不动,不随物体一起移动,因此均属于定滑轮。
本题答案为:定。
(2)首先,我们需要计算人的最大拉力,这个拉力应等于人的重力,即$F = G = mg = 85kg × 10N/kg = 850N$。然后,我们需要计算一块金属块的重力,即$G_{金属} = m_{金属}g = 10kg × 10N/kg = 100N$。最后,我们通过人的最大拉力除以一块金属块的重力,得出他一次最多能拉起的金属块数量,即$n = \frac{F}{G_{金属}} = \frac{850N}{100N} = 8.5$。由于金属块数量必须是整数,所以他一次最多能拉起8块金属块。
(3)当选择6块金属块时,我们需要先计算这些金属块的总重力,即$G_{总} = n_{金属}G_{金属} = 6 × 100N = 600N$。由于使用的是定滑轮,所以拉力等于重力,即$F_{拉} = G_{总} = 600N$。然后,我们利用功的公式$W = Fs$,将拉力和拉杆移动的距离代入公式,得出拉力做的功,即$W = F_{拉}s = 600N × 0.5m = 300J$。
【答案】:
(1)定 ;(2)8 ;(3)300J。