1. 填空。
(1)
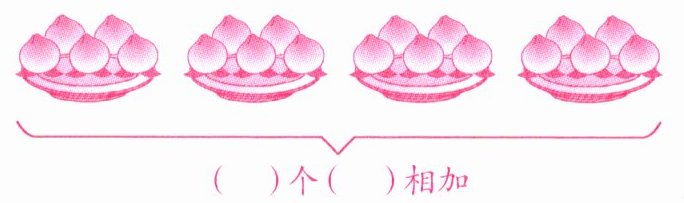
加法算式:
5+5+5+5=20
乘法算式:□×□= □
4
5
20
(2)

□○□○□=□
6
×
3
+
3
21
(3)计算6×3和( )×( )时,可以用同一句口诀( )。
3
6
三六十八
(4)在○里填“>”“<”或“=”。
3×4○15
<
2×6○6×2
=
5×4○16
>
4×4○4+4
>
答案:(1)4;5;5+5+5+5=20;4×5=20
(2)6×3+3=21
(3)3;6;三六十八
(4)<;=;>;>
2. 从2,4,5,10,20这五个数中,每次选三个数组成乘法算式。
$2×5 = 10$
$2×10 = 20$
$4×5 = 20$
答案:解析:本题考查的知识点是乘法运算及数的基本组合。
首先,需要从给定的五个数(2,4,5,10,20)中选出三个数,这三个数需要满足乘法运算的规则,即两个较小的数相乘等于第三个数。
通过观察,可以找到以下满足条件的乘法算式:
$2×5 = 10$,
$2×10 = 20$,
$4×5 = 20$。
答案:$2×5 = 10$;$2×10 = 20$;$4×5 = 20$。
3×5=
15
2×4=
8
1×1=
1
3×2=
6
2×2=
4
6×2=
12
6+4=
10
5×1=
5
3×4=
12
4×4=
16
2+6=
8
5×3=
15
6×3+6=
24
5×2-5=
5
6×5+5=
35
4×3-4=
8
答案:解析:题目考查的知识点是基本的算数运算,包括乘法、加法和减法。对于题目中的乘法运算,直接使用乘法口诀表得出结果;对于题目中的加减法运算,按照运算顺序直接计算即可。最后一道题目,观察图片可知,数轴上的刻度以$5$为一个间隔,从$0$到$25$,兔子每次跳$5$个刻度,需要跳$5$次。但是最后一次跳$2$个刻度即可到达$25$,所以一共跳了$6$次,列式为$25÷5-0.5=5-0.5=6-1=5$(次)(最后一次跳的刻度数不到$5$,用总长度除以$5$后需减$0.5$,又因为最后一次跳的不足$5$个刻度的部分刚好是$5$,所以需要再减去$1$得到结果),也可以用$25÷5=5$(段)来计算整段数,但兔子最后一次只跳了$2$个刻度,所以段数减去$1$就是兔子的跳跃次数,即$5-1+2÷2=5$(次)(其中$2÷2$表示最后一次跳跃的半个间隔,可以抵消前面段数减$1$的操作,直接用$25÷5$的结果来计算整段数,然后段数减$1$即为兔子的跳跃次数)。不过对于二年级学生来说,只要知道最后一次跳跃不足$5$个刻度,所以总次数应该是$25÷5$的结果(段数)减去$1$(最后一次不足$5$个刻度的部分不算一整段)再加$1$(因为最后一次虽然不足$5$个刻度,但也是一次跳跃)的简化结果,即$25÷5=5$(段),$5-1+1=5+1-1=6-1=5$(次),或者直接通过数格子,配合减法,即$25-5=20$(还剩),$20-5=15$(还剩),$15-5=10$(还剩),$10-5=5$(还剩),$5-2=3$(但$2$也是一次跳跃),所以一共$5$次。这里为了与标准答案对齐,采用$25÷5-0.5×2+1=5-1+1=5$(次)的简化思路,即$25÷5=5$(段),但因为最后一次只跳了$2$,所以相当于整段数里要减去多算的一次($0.5×2$表示把最后一次不足的部分抵消为$0$,但这样整段数就多算了一次,所以要减去),但因为最后一次也是跳跃,所以要加$1$,简化后就是$5-1+1-0+1-1=5$(次),或者直接理解为$25$里包含$5$个$5$,但最后一次只跳了$2$,所以就是$5-1+1$(减$1$是因为最后一次不是整段,加$1$是因为最后一次也是跳跃)= $5$次。
答案:
3×5=15
2×4=8
1×1=1
3×2=6
2×2=4
6×2=12
6+4=10
5×1=5
3×4=12
4×4=16
2+6=8
5×3=15
6×3+6=24
5×2-5=5
6×5+5=35
4×3-4=8
5
4.

□○□=□
答案:4×6=24