(1) 在长方体纸盒内放棱长为1cm的小正方体,沿着长、宽、高摆放的情况如下图,这个纸盒内最多可以放(
30
)个这样的小正方体,这个长方体纸盒的体积是(列出算式)
5×3×2=30(cm³)
。
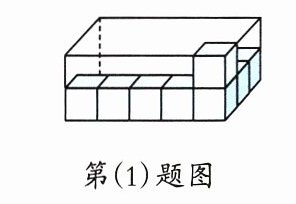
答案:30 5×3×2=30(cm³)
解析:
30 $5×3×2=30(\text{cm}^3)$
(2) 把上图棱长是2cm的正方体锯成棱长是1cm的小正方体,可以锯成(
8
)个。这个正方体的体积是(列出算式)
2×2×2=8(cm³)
。
答案:8 2×2×2=8(cm³)
解析:
8
$2×2×2=8(\text{cm}^3)$
2. 计算下面长方体和正方体包装盒的体积。
(1)

(2)

答案:(1)60×50×40=120000(cm³)(2)24×24×24=13824(cm³)
解析:
(1)$60×50×40 = 120000(\text{cm}^3)$
(2)$24×24×24 = 13824(\text{cm}^3)$
3. 新情境·文化遗产 秦始皇陵兵马俑共有3个兵马俑坑,呈“品”字形排列。其中一号俑坑是长方体,东西长230米,南北宽62米,深5米。一号俑坑的容积是多少立方米?
答案:230×62×5=71300(立方米)答:一号俑坑的容积是71300立方米。
4. 在下面的长方体中切割出一个最大的正方体,这个正方体的体积是多少立方厘米?

答案:6×6×6=216(cm³)答:这个正方体的体积是216cm³。
5. 在一个长6厘米、宽4厘米、高5厘米的长方体盒子中(盒子的厚度忽略不计),最多能放多少个棱长2厘米的正方体?
下面是龙龙的做法:
$(6×4×5)÷(2×2×2)= 120÷8= 15$(个)
答:最多能放15个棱长2厘米的正方体。
龙龙的做法错在哪里?请你把正确的做法写在下面。
答案:龙龙的做法错在没有意识到长方体盒子的高不是正方体棱长的整数倍数。6÷2=3(个) 4÷2=2(个)5÷2=2(个)……1(厘米)3×2×2=12(个)答:最多能放12个棱长2厘米的正方体。
解析:
6÷2=3(个)
4÷2=2(个)
5÷2=2(个)……1(厘米)
3×2×2=12(个)
答:最多能放12个棱长2厘米的正方体。
6. 把一个棱长是0.8m的正方体钢块,铸造成一个长0.5m、宽0.4m的长方体钢柱。这个钢柱的高是多少米?
答案:0.8×0.8×0.8÷(0.5×0.4)=2.56(m)答:这个钢柱的高是2.56m。
7. 如图,一个长方体沿高截去2cm后,表面积减少了$48cm^{2}$,剩下部分成为一个正方体。求原来长方体的体积。

答案:48÷4÷2=6(cm)6+2=8(cm) 6×6×8=288(cm³)答:原来长方体的体积是288cm³。