1. 先把等量关系式填写完整,再列方程解答。
李老师在电脑上下载一份文件,已经下载了340MB,还剩32%没有下载。这份文件一共有多大?
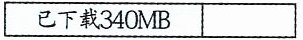
(
文件
)的容量 - (
没有下载
)的容量 = (
已经下载
)的容量
解:设这份文件一共有x MB。x-32%x=340 x=500 答:这份文件一共有500 MB。
答案:文件的 没有下载 已经下载 解:设这份文件一共有x MB。x-32%x=340 x=500 答:这份文件一共有500 MB。【点拨】直接根据题意找出等量关系式,再根据等量关系式列出方程并解答。
解析:
文件的 没有下载 已经下载 解:设这份文件一共有$x$ MB。$x - 32\%x = 340$,$0.68x = 340$,$x = 500$ 答:这份文件一共有500 MB。
2. 看图列方程计算。

答案:(1-40%)x=72 x=120
解析:
解:设一共有$x$吨。
$(1 - 40\%)x=72$
$x = 120$
3. 新考法·对比练习 华华是刚毕业的大学生,为了缓解租房压力,她决定和同事整租一套两室一厅的房子,住主卧的租金按整租的60%来收取。
(1) 如果华华住次卧,每月要付租金600元。她们整租的这套房子每月一共要付租金多少元?
(2) 如果华华住主卧,每月要付租金900元,那么她们整租的这套房子每月一共要付租金多少元?
答案:
(1)解:设她们整租的这套房子每月一共要付租金x元。x-60%x=600 x=1500 答:她们整租的这套房子每月一共要付租金1500元。【点拨】总租金-住主卧的租金=住次卧的租金。
(2)解:设她们整租的这套房子每月一共要付租金y元。60%y=900 y=1500 答:她们整租的这套房子每月一共要付租金1500元。【点拨】整租这套房子的租金×60%=主卧租金。
4. 三个工程队共同修完一条公路。下面是三位队长的一段对话:
甲队长说:“我们完成了全部任务的一半。”
乙队长说:“我们承担了全长的20%。”
丙队长说:“我们修了150米。”
请根据以上信息,算一算这条公路长多少米。
(列方程解)
答案:解:设这条公路长x米。x-50%x-20%x=150 x=500 答:这条公路长500米。【点拨】全长-甲队修的长度-乙队修的长度=丙队修的长度。
解析:
解:设这条公路长$x$米。
$x - 50\%x - 20\%x = 150$
$30\%x = 150$
$x = 500$
答:这条公路长500米。
5. 天天沿着一块等边三角形草坪的边散步(如图),他从A点出发经过B点走到D点,共行了这块草坪周长的45%。已知线段BD长21米,那么这块草坪的周长是多少米?

答案:解:设这块草坪的周长是x米。45%x-$\frac{1}{3}$x=21 x=180 答:这块草坪的周长是180米。
解析:
解:设这块草坪的周长是$x$米。
$45\%x - \frac{1}{3}x = 21$
$\frac{9}{20}x - \frac{1}{3}x = 21$
$\frac{27}{60}x - \frac{20}{60}x = 21$
$\frac{7}{60}x = 21$
$x = 21 × \frac{60}{7}$
$x = 180$
答:这块草坪的周长是180米。
6. 李爷爷准备用一根粗细均匀的竹竿做一个竹板凳,他从左端量到1.2米处做一个记号A,再从右端量到1.2米处做一个记号B,这时,他发现记号A、B之间的长度恰好是全长的20%。这根竹竿的长度是多少米?
答案:情况一:(1.2+1.2)÷(1-20%)=3(米)情况二:(1.2+1.2)÷(1+20%)=2(米)答:这根竹竿的长度是3米或2米。【点拨】情况一:这根竹竿的总长度大于两次量出的长度和,则这根竹竿的长度=(第一次量出的长度+第二次量出的长度)÷(1-20%)。情况二:这根竹竿的总长度小于两次量出的长度和,则这根竹竿的长度=(第一次量出的长度+第二次量出的长度)÷(1+20%)。
解析:
情况一:$(1.2 + 1.2) ÷ (1 - 20\%) = 3$(米)
情况二:$(1.2 + 1.2) ÷ (1 + 20\%) = 2$(米)
答:这根竹竿的长度是3米或2米。