4. 解决问题。
(1)新情境·文化遗产微刻是微观雕刻的一种,其中备受瞩目的作品有“怀禅八大刻”等。怀禅微刻《增广贤文》长3.5厘米,宽3.5厘米,高12厘米。
①给怀禅微刻《增广贤文》做了一个礼品盒,礼品盒比这一微刻作品的前、后、左、右各宽0.75厘米,上、下各高1厘米,制作这个礼品盒至少用了多少平方厘米的木板？
礼品盒的高：12+1+1=14（厘米）
礼品盒的长、宽：3.5+0.75+0.75=5（厘米）
礼品盒所用木板：
14×5×4+5×5×2=330（平方厘米）
答：制作这个礼品盒至少用了330平方厘米的木板。
②这个礼品盒的容积最多是多少立方厘米？
14×5×5=350（立方厘米）
答：这个礼品盒的容积最多是350立方厘米。
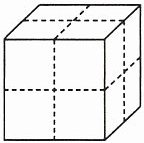
(2)木匠王师傅用传统手艺制作木制积木。他将一个表面积为24平方厘米的正方体木块用锯子均匀地切割三次(如图),得到8个大小相同的小正方体木块,它们的表面积之和比原来正方体木块的表面积增加了多少平方厘米？

24÷6=4（平方厘米）
4×6=24（平方厘米）
答：它们的表面积之和比原来正方体木块的表面积增加了24平方厘米。
(3)聪聪为了测量一个桃子的体积,设计了下面的实验步骤,但被打乱了顺序。
a.列式计算出桃子的体积。
b.找一个长方体无盖透明塑料容器,量得底面长8厘米,宽6厘米,高30厘米。
c.将桃子完全浸没在水中,量出水面高度22厘米。
d.倒入适量的水,量出水面高度15厘米。
①正确的实验顺序应该是→→→。(填字母)
②这个桃子的体积是多少立方厘米？
8×6×（22-15）=336（立方厘米）
答：这个桃子的体积是336立方厘米。
(4)李叔叔制作了底部用阀门和细水管连通的两个水槽(如图),从里面量,分别是长6分米、宽4分米、水深3分米的甲水槽和空着的长3分米、宽和高都是2分米的乙水槽。现在打开阀门,直到两个水槽中的水面同样高,此时甲、乙两个水槽中的水面高多少分米？(细水管内的水忽略不计)

（6×4×3）÷（6×4+3×2）=2.4（分米）
答：此时甲、乙两个水槽中的水面高2.4分米。
(5)用一张长40厘米、宽20厘米的长方形铁皮做一个深5厘米的无盖长方体容器(焊接处和铁皮厚度忽略不计)。如图三种焊接方法中,按哪种方法焊接后做成的长方体容器的容积最大？

①（40-5×2）×（20-5×2）×5=1500（立方厘米）
②（40-5）×（20-5×2）×5=1750（立方厘米）
③（40÷2）×（40÷2）×（20÷4）=2000（立方厘米）
2000＞1750＞1500
答：按第③种方法焊接后做成的长方体容器的容积最大。