(1) 一个三角形的底扩大到原来的3倍,高扩大到原来的2倍,面积就扩大到原来的(
6
)倍。
答案:6
解析:
三角形面积公式为$S = \frac{1}{2}ah$(其中$a$为底,$h$为高)。底扩大到原来的3倍变为$3a$,高扩大到原来的2倍变为$2h$,新面积$S'=\frac{1}{2}×3a×2h = 3ah$。原面积$S=\frac{1}{2}ah$,则$\frac{S'}{S}=\frac{3ah}{\frac{1}{2}ah}=6$。6
(2) 张爷爷承包了一片形似直角梯形的湖泊养鱼。已知湖泊的上底与下底的和是1000米,两条腰分别长4000米和6000米,这个梯形的面积是(
2000000
)平方米,合(
200
)公顷,(
2
)平方千米。
答案:2000000 200 2
解析:
直角梯形的高小于斜腰,故高为4000米。
面积:$1000×4000÷2 = 2000000$(平方米)
2000000平方米 = 200公顷 = 2平方千米
2000000 200 2
(3) 如图,一个长方形框架,把它拉成一个高为20cm的平行四边形,该平行四边形的周长是(
112
)cm,面积是(
600
)$cm^{2}$。
答案:112 600
(4) 古代数学名著《九章算术》中记载了三角形的面积计算方法是“半广以乘正从”。如果三角形的底是10厘米,高是12厘米,那么转化成的长方形的长是(
12
)厘米,宽是(
5
)厘米,面积是(
60
)平方厘米。
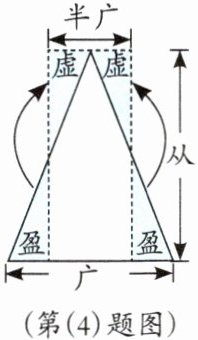
答案:12 5 60 [点拨]转化成的长方形的长是12厘米,宽是10÷2=5(厘米),面积是12×5=60(平方厘米)。
(5) 如下图,在直角三角形ABC中,涂色部分的面积是12平方厘米,D、E分别是BC、AC的中点,则三角形ABC的面积是(
48
)平方厘米。
答案:48 [点拨]将涂色部分三角形ADE的面积看作1份,因为E是AC的中点,所以三角形CDE与它等底等高,面积也是1份。这样,三角形ADC的面积就是2份,因为D是BC的中点,三角形ABD与三角形ADC等底等高,面积也是2份,所以三角形ABC的面积是这样的4份,用12×4=48(平方厘米)即可解答。
解析:
因为E是AC的中点,所以AE=EC,三角形ADE和三角形CDE等底等高,面积相等,均为12平方厘米。则三角形ADC的面积为12+12=24平方厘米。
因为D是BC的中点,所以BD=DC,三角形ABD和三角形ADC等底等高,面积相等,均为24平方厘米。则三角形ABC的面积为24+24=48平方厘米。
48
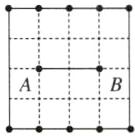
(1) 如下图,在给定的正方形方格顶点上(每个小方格表示1平方厘米)找一点C,使三角形ABC的面积是2平方厘米,点C共有( )种不同的画法。

A.5
B.6
C.8
D.10
答案:D [点拨]因为要使三角形ABC的面积为2平方厘米,所以三角形ABC的底边AB上的高应为2×2÷2=2(厘米),即点C到线段AB的距离为2厘米。点C可以在线段AB的上方,也可以在线段AB的下方,如图:
(2) 典典运用“割、补”的方法计算下面组合图形的面积,下列算式中,(
D
)能够表达他的其中一个方法。(单位:cm)

A.$(9 + 30)×20÷2$
B.$30×12 + (9 + 30)×(20 - 12)$
C.$(9 + 30)×12÷2$
D.$30×20 - (30 - 9)×(20 - 12)÷2$
答案:D
3. 华华参加了某室外音乐节的志愿活动,她正在统计观众人数。(每个小方格的边长表示10米)
(1) 她用“$(30 + 50)×60÷2$”算出了音乐节舞台前的观众区的面积。请在右面的方格纸上画出这个观众区可能的形状。

(2) 相关研究表明,室内景点人均活动面积低于1平方米,室外景点人均活动面积低于0.75平方米时,就有发生踩踏事故的危险。

答案:(1)(答案不唯一)

(2)(30+50)×60÷2=2400(平方米)
2400÷0.75=3200(人)
答:这个观众区最多能容纳3200人同时观看节目。
4. 聪聪用“几何画板”软件对底和高都是6厘米的三角形ABC进行操作(如下图),从点A分离出点$A'$,点A不动,点$A'$和点C同时以1厘米/秒的速度向右平移,与原三角形组成一个梯形。几秒后梯形的面积是原来三角形面积的2倍?

答案:6×6÷2×2−6×6÷2=18(平方厘米)
18÷6=3(厘米)
3÷1=3(秒)
答:3秒后梯形的面积是原来三角形面积的2倍。
[点拨]点A'和点C同时以1厘米/秒的速度向右平移,增加的部分是一个高为6厘米的平行四边形,如下图。

先用梯形的面积减去原来三角形的面积求出新增平行四边形的面积,再用新增平行四边形的面积除以高求出新增平行四边形的底,也就是向右平移的长度,最后用平移的长度除以移动的速度求出平移的时间。