|图形编号|多边形内的钉子数/枚|多边形边上的钉子数/枚|多边形的面积/平方厘米|
|①|
1
|
6
|
3
|
|②|
1
|
6
|
3
|
|③|
1
|
5
|
2.5
|
|④|
1
|
8
|
4
|
(1) 这些多边形的共同特点是多边形内只有(
1
)枚钉子。
(2) 当多边形内只有 1 枚钉子时,这些多边形面积的平方厘米数是它们边上钉子数的(
一半
)。
(3) 当多边形内只有 1 枚钉子时,用 $ n $ 表示多边形边上的钉子数,用 $ S $ 表示多边形的面积,那么 $ S = $ (
n÷2
)。
答案:|①|1|6|3|②|1|6|3|③|1|5|2.5|④|1|8|4|
(1)1 (2)一半 (3)n÷2
2. 如图,在钉子板上围多边形,如果多边形内有 2 枚钉子,用 $ n $ 表示多边形边上的钉子数,用 $ S $ 表示多边形的面积,那么 $ S = $
D
。
A.$ (n - 2) ÷ 2 $
B.$ n ÷ 2 + 2 $
C.$ n ÷ 2 - 1 $
D.$ n ÷ 2 + 1 $
答案:D [点拨]通过观察可知,多边形的面积S与多边形边上的钉子数n和多边形内的钉子数a的关系是S=a+n÷2−1,代入题中数据,可知S=2+n÷2−1=n÷2+1。
3. 如图,在钉子板上围成四个图形,每个图形的面积是多少平方厘米?(横、竖每相邻两枚钉子之间的距离是 1 cm)
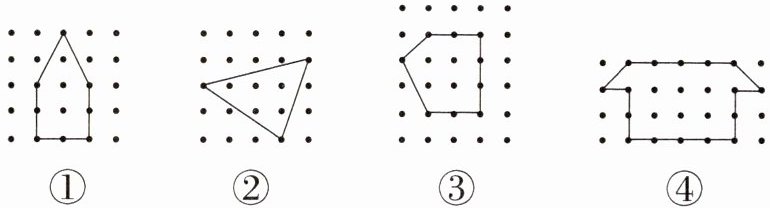
奥地利数学家乔治·亚历山大·皮克发现:格点多边形的面积 $ = $ 边界的格点数 $ ÷ 2 + $ 内部的格点数 $ - 1 $,这个发现也被称为“皮克定理”。
(1) ①号格点多边形的边界的格点数是 8,内部的格点数是 3,它的面积是(
6
)$ cm^{2} $。
(2) ②号格点多边形的边界的格点数是(
3
),内部的格点数是(
5
),它的面积是(
5.5
)$ cm^{2} $。
(3) ③号和④号格点多边形的面积相比较,(
④
)号格点多边形的面积大,请把比较的方法写在下面。
③号格点多边形的面积:9÷2+4−1=7.5(cm²)
④号格点多边形的面积:16÷2+6−1=13(cm²)
7.5<13
答案:(1)6
(2)3 5 5.5
(3)④
③号格点多边形的面积:9÷2+4−1=7.5(cm²)
④号格点多边形的面积:16÷2+6−1=13(cm²)
7.5<13
[点拨]根据题中的“格点多边形的面积=边界的格点数÷2+内部的格点数−1”进行计算。
4. 一个钉子板横、竖每相邻两枚钉子之间的距离都是 1 厘米,在这个钉子板上围了一个八边形,内部有 3 枚钉子,且面积为 6 平方厘米,则该八边形的边上有(
8
)枚钉子。
答案:8 [点拨]n÷2+a−1=6, 其中a=3, 则n÷2+3−1=6,n÷2=4,n=4×2=8。
解析:
根据毕克定理:$S = n÷2 + a - 1$(其中$S$为图形面积,$n$为边上钉子数,$a$为内部钉子数)。已知$S = 6$,$a = 3$,则$6 = n÷2 + 3 - 1$,$n÷2 = 4$,$n = 8$。
8
5. 在下面的点子图上,画出两个面积是 6 平方厘米且形状不同的多边形。(横、竖每相邻两个点之间的距离都是 1 厘米)

答案:画图如下:
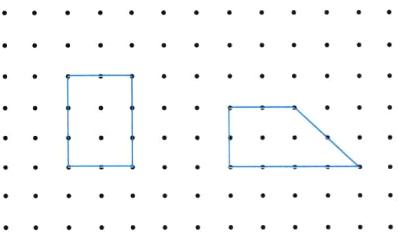
(答案不唯一)
[点拨]根据S=n÷2+a−1可得例如当a=2时,多边形边上的钉子数是(6+1−2)×2=10。