1.(2024·浙江杭州拱墅区期末)一元一次方程-3(x-1)= 5(x+2),去括号,得(
D
).
A.-3x-1= 5x+2
B.-3x-3= 5x+10
C.-3x+1= 5x+2
D.-3x+3= 5x+10
答案:D
解析:
解:对一元一次方程$-3(x - 1)=5(x + 2)$去括号,
左边:$-3 × x + (-3) × (-1)=-3x + 3$,
右边:$5 × x + 5 × 2=5x + 10$,
得$-3x + 3=5x + 10$。
D
2.(2025·淮安期末)下列各数是方程2025(x-1)+2= 2x的解是(
B
).
A.-1
B.1
C.-2
D.2
答案:B
解析:
2025(x-1)+2=2x
2025x-2025+2=2x
2025x-2x=2025-2
2023x=2023
x=1
B
3.解方程$4(x-1)-x= 2(x+\frac{1}{2}),$步骤如下:
①去括号,得4x-4-x= 2x+1;②移项,得4x+x-2x= 4+1;③合并同类项,得3x= 5;④系数化为1,得$x= \frac{5}{3}.$其中错误的一步是(
B
).
A.①
B.②
C.③
D.④
答案:B
解析:
解方程$4(x - 1)-x=2\left(x+\frac{1}{2}\right)$:
①去括号,得$4x - 4 - x=2x + 1$;
②移项,得$4x - x - 2x=4 + 1$;
③合并同类项,得$x=5$;
④系数化为1,得$x = 5$。
其中错误的一步是②。
B
答案:x=6
解析:
解:$2(x-3)=6$
$x-3=3$
$x=6$
5.已知代数式4-x与3(2-x)的值相等,则x的值为
1
.
答案:1
解析:
4-x=3(2-x)
4-x=6-3x
-x+3x=6-4
2x=2
x=1
6.教材P116例4·变式 去括号解一元一次方程$:(1)5x+2= 3(x+2);(2)3(y+2)-2(y-\frac{3}{2})= 5-4y.$
答案:
(1)5x+2=3(x+2),去括号,得5x+2=3x+6,移项,得5x-3x=6-2,合并同类项,得2x=4,系数化为1,得x=2.
(2)3(y+2)-2(y-$\frac{3}{2}$)=5-4y,去括号,得3y+6-2y+3=5-4y,移项,得3y-2y+4y=5-6-3,合并同类项,得5y=-4,系数化为1,得y=-$\frac{4}{5}$.
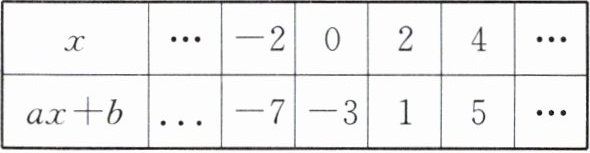
7.(2025·南京建邺区期末)如表是当x取不同值时,整式ax+b对应的值,则关于x的方程ax - b= 2025的解为(
D
).
| x | ... | -2 | 0 | 2 | 4 | ... |
| ax+b | ... | -7 | -3 | 1 | 5 | ... |
A.x= 1201
B.x= 1101
C.x= 1103
D.x= 1011
答案:D [解析]由表格中数据可知,当x=0时,ax+b=-3,
∴b=-3.当x=2时,ax+b=1,
∴2a-3=1,解得a=2,
∴2x-(-3)=2025,即2x+3=2025,移项、合并同类项,得x=1011.故选D.
8.中考新考法 过程纠错改错 (2025·贵州贵阳期末)小军解方程x+2(x-3)= 5x+2的过程如表所示:
解:去括号,得x+2x-6= 5x+2 ……………………………………… 第一步
移项,得x+2x+5x= 2-6 …… 第二步
合并同类项,得8x= -4 ……… 第三步
系数化为1,得$x= -\frac{4}{8} ……… $第四步
(1)小军的解答步骤是从第
二
步开始出错的;
(2)请你写出正确的解答过程.
解:去括号,得x+2x-6=5x+2,移项,得x+2x-5x=2+6,合并同类项,得-2x=8,系数化为1,得x=-4.
答案:
(1)二
(2)去括号,得x+2x-6=5x+2,移项,得x+2x-5x=2+6,合并同类项,得-2x=8,系数化为1,得x=-4.