1. 如果$x= y$,那么下列等式不一定成立的是(
D
).
A.$x+a= y+a$
B.$x-a= y-a$
C.$ax= ay$
D.$\frac{x}{a}= \frac{y}{a}$
答案:D
解析:
当$x = y$时:
选项A:根据等式性质1,等式两边同时加$a$,$x + a = y + a$成立;
选项B:根据等式性质1,等式两边同时减$a$,$x - a = y - a$成立;
选项C:根据等式性质2,等式两边同时乘$a$,$ax = ay$成立;
选项D:根据等式性质2,等式两边同时除以$a$,需满足$a \neq 0$,当$a = 0$时,$\frac{x}{a}$和$\frac{y}{a}$无意义,所以$\frac{x}{a} = \frac{y}{a}$不一定成立。
D
2.(2025·盐城阜宁期末改编)运用等式性质进行的变形,不正确的是(
C
).
A.如果$a= b$,那么$a-1= b-1$
B.如果$a= b$,那么$a+c= b+c$
C.如果$a= b$,那么$\frac{a}{c}= \frac{b}{c}$
D.如果$a= b$,那么$ac= bc$
答案:C
3.(2024·连云港海州区期末)如图,用“○”“△”及“□”代表3种不同物体,且前两个天平是平衡状态,现需在图(3)天平的“?”处放置
5
个“□”才能使得天平也平衡.
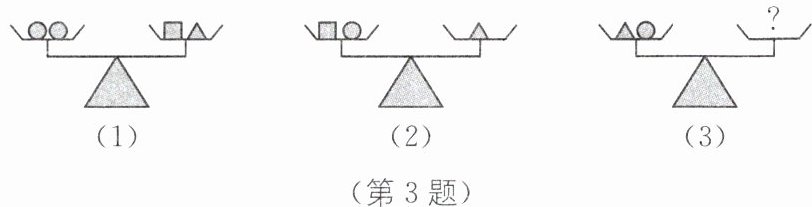
答案:5 [解析]由题图
(1)和题图
(2),得两个“●”的质量=两个“■”的质量+一个“●”的质量,则一个“●”的质量=两个“■”的质量,再由题图
(2)可得一个“▲”的质量=三个“■”的质量,那么一个“▲”的质量+一个“●”的质量=五个“■”的质量.
4. 教材P108练习T2·变式 利用等式的性质,将下面的等式变形为$x= c$($c$为常数)的形式.
(1)$3= x+5$;
(2)$-\frac{2}{3}x= 4$.
答案:
(1)x=-2
(2)x=-6
5. 根据等式的性质,下列变形正确的是(
D
).
A.如果$8a= 4$,那么$a= 2$
B.如果$ac= bc$,那么$a= b$
C.如果$\frac{a}{2}= \frac{b}{3}$,那么$2a= 3b$
D.如果$1-2a= 3a$,那么$3a+2a= 1$
答案:D [解析]如果8a=4,那么a= $\frac{1}{2}$,故A选项不符合题意;如果ac=bc(c≠0),那么a=b,故B选项不符合题意;如果$\frac{a}{2}=\frac{b}{3}$,那么3a=2b,故C选项不符合题意;如果1-2a=3a,那么3a+2a=1,故D选项符合题意.故选D.
6.(2025·镇江句容期末)下列等式变形正确的是(
A
).
A.若$a= b$,则$ac= bc$
B.若$ac= bc$,则$a= b$
C.若$a^2= b^2$,则$a= b$
D.若$-\frac{1}{3}x= 6$,则$x= -2$
答案:A [解析]若a=b,则ac=bc,故A选项符合题意;若ac=bc,当c≠0时,则a=b,故B选项不符合题意;若$a^2=b^2$,则a=±b,故C选项不符合题意;若$-\frac{1}{3}x=6$,则x=-18,故D选项不符合题意.故选A.
7. 在等式$3×□ - 2×□= 15$的两个方格内分别填入一个数,使这两个数互为相反数且等式成立,则第一个方格内的数为
3
.
答案:3 [解析]设第一个“□”为x,则第二个“□”为-x.依题意,得3x-2×(-x)=15,解得x=3.故第一个方格内的数是3.
解析:
设第一个“□”为$x$,则第二个“□”为$-x$。依题意,得$3x - 2×(-x) = 15$,解得$x = 3$。
3
8.(2025·盐城建湖期中)利用等式的基本性质,将下面的等式变形为$x= c$($c$为常数)的形式.
(1)$5x-3= 7$;
(2)$\frac{1}{2}x - 2= 2x+7$.
答案:
(1)5x-3=7,方程两边同时加上3,得5x=10,→利用等式的基本性质1方程两边同时除以5,得x=2.→利用等式的基本性质2
(2)$\frac{1}{2}x-2=2x+7$,方程两边同时减去7,得$\frac{1}{2}x-9=2x$,方程两边同时减去$\frac{1}{2}x$,得-9=$\frac{3}{2}x$,方程两边同时除以$\frac{3}{2}$,得x=-6.
9.(2025·河北邢台信都区期末)在将等式$3x-2y= 2x-2y$变形时,小明的变形过程如下:因为$3x-2y= 2x-2y$,所以$3x= 2x$,(第一步)所以$3= 2$.(第二步)
(1)上述过程中,第一步的依据是什么?
(2)小明第二步的结论正确吗?请说明原因.
答案:
(1)
∵3x-2y=2x-2y,
∴根据等式的性质1,两边都加上2y,得3x=2x,
∴第一步的依据是等式的性质1.
(2)小明第二步的结论不正确,理由如下:
∵根据等式的性质2,等式两边同时除以不为0的两个数,等式仍然成立,
∴当x=0时,等式的两边都除以x,等式不成立,
∴小明第二步的结论不正确.