1. 观察以下等式,寻找等式中的规律:
(1)等式 1: $2×4 + 1 = 9 = 3^2$;
等式 2: $6×8 + 1 = 49 = 7^2$;
等式 3: $10×12 + 1 = 121 = 11^2$;…
①请写出第 4 个等式:
14×16+1=225=15²
;
②请写出第 n 个等式:
(4n-2)·(4n)+1=16n²-8n+1=(4n-1)²
;
(2)第 1 个等式:$\frac{1}{3}×(1 + \frac{2}{1}) = 2 - \frac{1}{1}$;
第 2 个等式:$\frac{5}{5}×(1 + \frac{2}{3}) = 2 - \frac{1}{3}$;
第 3 个等式:$\frac{9}{7}×(1 + \frac{2}{5}) = 2 - \frac{1}{5}$;
第 4 个等式:$\frac{13}{9}×(1 + \frac{2}{7}) = 2 - \frac{1}{7}$;
第 5 个等式:$\frac{17}{11}×(1 + \frac{2}{9}) = 2 - \frac{1}{9}$;…
③请写出第 6 个等式:
$\frac{21}{13}×(1+\frac{2}{11})=2-\frac{1}{11}$
;
④请写出第 n 个等式:
$\frac{4n-3}{2n+1}(1+\frac{2}{2n-1})=2-\frac{1}{2n-1}$
.
答案:①14×16+1=225=15² ②(4n-2)·(4n)+1=16n²-8n+1=(4n-1)² ③$\frac{21}{13}×(1+\frac{2}{11})=2-\frac{1}{11}$ ④$\frac{4n-3}{2n+1}(1+\frac{2}{2n-1})=2-\frac{1}{2n-1}$
2. 如图,下列各正方形中的四个数之间具有相同的规律.
(1)
| -1 | -1 |
| -2 | 2 |
(2)
| 2 | 14 |
| 4 | 8 |
(3)
| -4 | -16 |
| -8 | -4 |
(4)
| 8 | 44 |
| 16 | 20 |
…
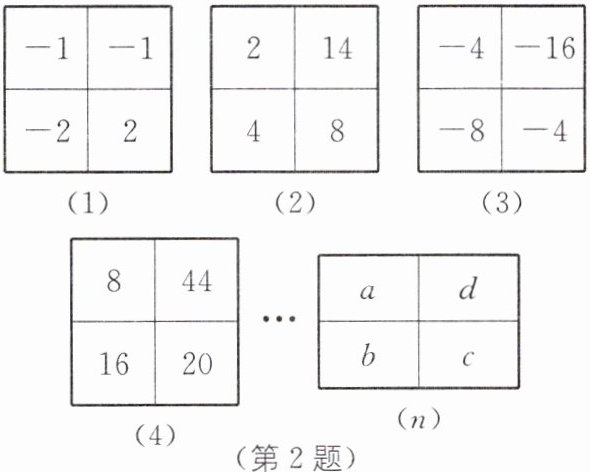
(n)
| a | d |
| b | c |
根据此规律,则图(n)中的 $c=$______(用含 a,b,d 的式子表示).
d-a-b
答案:d-a-b [解析]第1个图:-1-(-1-2)=2;第2个图:14-(2+4)=8;第3个图:-16-(-4-8)=-4;第4个图:44-(8+16)=20;…;第n个图:d-(a+b)=c,所以c=d-a-b.
3. 用正方形按如图所示的规律拼图案,其中第①个图案中有 5 个正方形,第②个图案中有 9 个正方形,第③个图案中有 13 个正方形,第④个图案中有 17 个正方形,以此规律排列下去,则第⑨个图案中正方形的个数为(
C
).

A.32
B.34
C.37
D.41
答案:C
解析:
第①个图案:5个
第②个图案:9个,9=5+4
第③个图案:13个,13=9+4
第④个图案:17个,17=13+4
规律:后一个图案比前一个多4个正方形,第n个图案中正方形个数为 $5 + 4(n - 1) = 4n + 1$
第⑨个图案:$4×9 + 1 = 37$
C
4. 如图是用棋子摆成的“上”字图案,按照这种规律继续摆下去,通过观察、对比、总结,找出规律,解答下列问题.

(1)摆成图(1)需要
6
枚棋子,摆成图(2)需要
10
枚棋子,摆成图(3)需要
14
枚棋子.
(2)摆成图(n)需要
(4n+2)
枚棋子.
(3)七(1)班有 46 名同学,把每名同学当成一枚“棋子”,能否让这 46 枚“棋子”按照以上规律恰好站成一个“上”字?若能,请问能站成图几?并计算最下面一“横”的学生数;若不能,请说明理由.
能,能站成题图(11). 由题意知,4n+2=46,解得n=11. 最下面一“横”的学生数为2n+1=23.
答案:
(1)6 10 14 [解析]第
(1)个图形中有6个棋子;第
(2)个图形中有6+4=10(个)棋子;第
(3)个图形中有6+2×4=14(个)棋子.
(2)(4n+2)
(3)能,能站成题图
(11). 由题意知,4n+2=46,解得n=11. 最下面一“横”的学生数为2n+1=23.