2025年实验班提优训练七年级数学上册苏科版第165页解析答案

25. (2025·连云港东海期末)[习题再现]
(1)苏科版初中数学教材七上第194页第10题：如图(1),$AB // CD$,点E在AB,CD之间.写出$\angle AEC$,$\angle A$,$\angle C$之间的数量关系,并说明理由；
[迁移思考]
(2)小明在完成第10题的探究后,对该页的第5题又作了探究与变式思考：
①如图(2),在长方体盒子底部有一面平面镜,点A处有一个光源,光线的入射角等于反射角,法线OE与平面镜l垂直,即$OE \perp BC$,垂足为O,入射光线经过镜面反射后,恰好经过点D.小明认为,图中$\angle AOB= \angle COD$,请帮小明说明理由；
②如图(3),在长方体盒子里放置4块平面镜AB,BC,CD,DA,其中$AD // CB$,若光线从AD上的E处射出,在平面镜AB上经点F反射后,到达BC上的点G,其传播路径为E→F→G→H→E→F…,请判断$\angle EFG与\angle GHE$的数量关系,并说明理由.

答案：

(1)∠AEC,∠A,∠C之间的数量关系是∠AEC = ∠A + ∠C.理由如下:过点E作EM//AB,如图所示.

∵AB//CD,
∴AB//EM//CD,
∴∠AEM = ∠A,∠CEM = ∠C,
∴∠AEM + ∠CEM = ∠A + ∠C.
∵∠AEC = ∠AEM + ∠CEM,
∴∠AEC = ∠A + ∠C.
(2)①∠AOB = ∠COD.理由如下:
∵OE⊥BC,
∴∠EOC = ∠EOB = 90°,
∴∠AOE + ∠AOB = ∠DOE + ∠COD = 90°.
∵光线的入射角等于反射角,
∴∠AOE = ∠DOE,
∴∠AOB = ∠COD.②∠EFG与∠GHE的数量关系是∠EFG = ∠GHE.理由如下:由①的结论得∠AEF = ∠DEH,∠BGF = ∠CGH,
∴∠AEF + ∠BGF = ∠DEH + ∠CGH.
∵AD//CB,由
(1)的结论,得∠EFG = ∠AEF + ∠BGF,∠EHG = ∠DEH + ∠CGH,
∴∠EFG = ∠EHG.

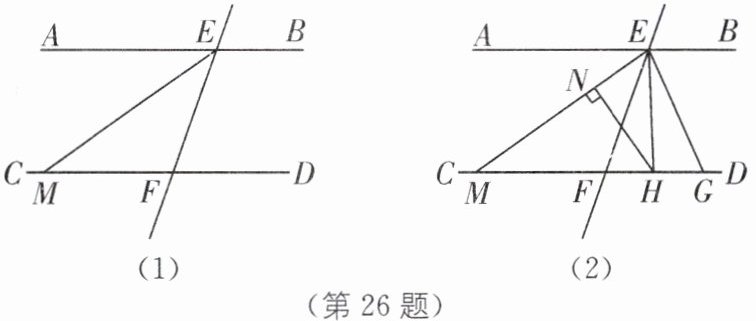
26. 如图(1),已知两条直线AB,CD被直线EF所截,分别交于点E,F,EM平分$\angle AEF$交CD于点M,且$\angle FEM= \angle FME$.
(1)判断直线AB与直线CD是否平行,并说明理由.
(2)如图(2),点G是射线MD上一动点(不与点M,F重合),EH平分$\angle FEG$交CD于点H,过点H作$HN \perp EM$于点N,设$\angle EHN= \alpha$,$\angle EGF= \beta$.
①当点G在点F的右侧时,若$\beta=50^\circ$,求α的度数.
②当点G在运动过程中,α和β之间有怎样的数量关系？请写出你的猜想,并加以说明.

答案：

(1)AB//CD,理由如下:
∵EM平分∠AEF,
∴∠AEM = ∠MEF.又∠FEM = ∠FME,
∴∠AEM = ∠EMF,
∴AB//CD.
(2)①
∵AB//CD,β = 50°,
∴∠AEG = 130°.又EH平分∠FEG,EM平分∠AEF,
∴∠HEF = $\frac{1}{2}$∠FEG,∠MEF = $\frac{1}{2}$∠AEF,
∴∠MEH = $\frac{1}{2}$∠AEG = 65°.又HN⊥ME,
∴∠EHN = 90° - 65° = 25°,即α = 25°;②α = $\frac{1}{2}$β或α = 90° - $\frac{1}{2}$β,理由如下:分两种情况讨论:当点G在点F的右侧时,α = $\frac{1}{2}$β.
∵AB//CD,
∴∠AEG = 180° - β.又EH平分∠FEG,EM平分∠AEF,
∴∠HEF = $\frac{1}{2}$∠FEG,∠MEF = $\frac{1}{2}$∠AEF,
∴∠MEH = $\frac{1}{2}$∠AEG = $\frac{1}{2}$(180° - β).又HN⊥ME,
∴∠EHN = 90° - ∠MEH = 90° - $\frac{1}{2}$(180° - β) = $\frac{1}{2}$β,即α = $\frac{1}{2}$β;如图,当点G在点F的左侧时,α = 90° - $\frac{1}{2}$β.

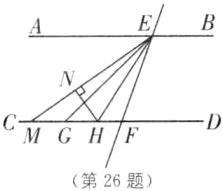
∵AB//CD,
∴∠AEG = ∠EGF = β.又EH平分∠FEG,EM平分∠AEF,
∴∠HEF = $\frac{1}{2}$∠FEG,∠MEF = $\frac{1}{2}$∠AEF,
∴∠MEH = ∠MEF - ∠HEF = $\frac{1}{2}$(∠AEF - ∠FEG) = $\frac{1}{2}$∠AEG = $\frac{1}{2}$β.又HN⊥ME,
∴∠EHN = 90° - ∠MEH,即α = 90° - $\frac{1}{2}$β.综上所述,α = $\frac{1}{2}$β或α = 90° - $\frac{1}{2}$β.