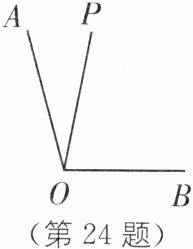
24. 动角模型 中考新考法 新定义问题 如图(1),射线OP在$\angle AOB$的内部($\angle AOB的度数大于0^\circ且小于180^\circ$),图中共有三个角:$\angle AOP$,$\angle POB$,$\angle AOB$.若这三个角中有两个角的度数之比为3:1,则称射线OP为$\angle AOB$的“虚学线”.
(1)$\angle AOB$的平分线______$\angle AOB$的“虚学线”,$\angle AOB$的一条三等分线______$\angle AOB$的“虚学线”;(填“是”或“不是”)
(2)射线OP为$\angle AOB$的“虚学线”,若$\angle AOP= 30^\circ$,求$\angle AOB$的度数;
(3)已知$\angle AOB= 160^\circ$,射线OC从OA出发,绕O点以每秒$15^\circ$按顺时针方向旋转,射线OD从OB出发,绕O点以每秒$10^\circ$按逆时针方向旋转,两条射线同时旋转,当射线OC与OB重合时,旋转停止.设旋转时间为t秒,射线OE为$\angle COD$的平分线,射线OA,OD,OE中,若其中一条射线是另两条射线组成的角的“虚学线”,直接写出所有t的值.

答案:(1)不是 是
(2)由一个角的“虚学线”的定义可知,当∠AOP = $\frac{1}{3}$∠AOB或∠AOP = $\frac{2}{3}$∠AOB或∠AOP = $\frac{1}{3}$∠BOP或∠AOP = 3∠BOP时,射线OP是∠AOB的“虚学线”当∠AOP = $\frac{1}{3}$∠AOB时,由∠AOP = 30°,得∠AOB = 3×30° = 90°;当∠AOP = $\frac{2}{3}$∠AOB时,由∠AOP = 30°,得∠AOB = $\frac{3}{2}$×30° = 45°;当∠AOP = $\frac{1}{3}$∠BOP时,由∠AOP = 30°,得∠BOP = 3×30° = 90°,
∴∠AOB = 30° + 90° = 120°;当∠AOP = 3∠BOP时,得∠BOP = 10°,
∴∠AOB = 30° + 10° = 40°.综上所述,∠AOB的度数为45°或90°或120°或40°.
(3)由题意,得∠AOC = 15t°,∠BOD = 10t°,当OC与OD重合前,旋转的时间t秒的取值范围为0 ≤ t < $\frac{160}{15 + 10}$,即0 ≤ t < 6.4,如图
(1),
∵OE平分∠COD,
∴∠COE = ∠DOE = $\frac{1}{2}$∠COD = $\frac{1}{2}$(160 - 10t - 15t)° = ($\frac{160 - 25t}{2}$)°.由于∠AOE > ∠DOE,则当∠AOE = 2∠DOE或∠AOE = 3∠DOE时,射线OE是∠AOD的“虚学线”,即15t + $\frac{160 - 25t}{2}$ = $\frac{160 - 25t}{2}$×2或15t + $\frac{160 - 25t}{2}$ = $\frac{160 - 25t}{2}$×3,解得t = $\frac{32}{11}$或t = 4;
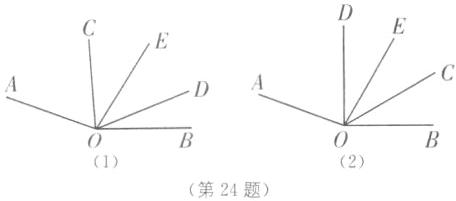
当OC与OD重合后,旋转的时间t秒的取值范围为6.4 < t ≤ $\frac{160}{15}$,即6.4 < t ≤ $\frac{32}{3}$,如图
(2).
∵OE平分∠COD,
∴∠COE = ∠DOE = $\frac{1}{2}$∠COD = $\frac{1}{2}$(10t + 15t - 160)° = ($\frac{25t - 160}{2}$)°.当∠AOD = 2∠DOE或∠AOD = 3∠DOE时,射线OD是∠AOE的“虚学线”,即160 - 10t = 2×$\frac{25t - 160}{2}$或160 - 10t = 3×$\frac{25t - 160}{2}$,解得t = $\frac{64}{7}$或t = $\frac{160}{19}$;当2∠AOD = ∠DOE或3∠AOD = ∠DOE时,射线OD是∠AOE的“虚学线”,即2(160 - 10t) = $\frac{25t - 160}{2}$或3(160 - 10t) = $\frac{25t - 160}{2}$,解得t = $\frac{160}{13}$ > $\frac{160}{15}$(舍去)或t = $\frac{224}{17}$ > $\frac{160}{15}$(舍去),综上所述,当射线OA,OD,OE中的一条射线是另两条射线组成的角的“虚学线”时,t的值为$\frac{32}{11}$或4或$\frac{64}{7}$或$\frac{160}{19}$.