14. 中考新考法 规律探究 木材加工厂将一批木料按如图所示的规律依次摆放,则第n个图中共有木料
$\frac{n(n+1)}{2}$
根.
答案:$\frac{n(n+1)}{2}$[解析]由题图可知,第1个图形有木料1根;第2个图形有木料$1+2=3$(根);第3个图形有木料$1+2+3=6$(根);第4个图形有木料$1+2+3+4=10$(根);……,则第n个图形有木料$1+2+3+4+\cdots +n=\frac{n(n+1)}{2}$(根).
15.(2025·无锡江阴期中)如图所示是计算机程序计算,若开始输入$x= -1$,则最后输出的结果是
-11
.
答案:-11 [解析]把$x=-1$代入计算程序中,得$(-1)×4-(-1)=-4+1=-3>-5;$把$x=-3$代入计算程序中,得$(-3)×4-(-1)=-12+1=-11<-5,$则最后输出的结果是-11.
解析:
把$x = -1$代入计算程序,得$(-1)×4 - (-1) = -4 + 1 = -3$,因为$-3 > -5$,所以返回输入;把$x = -3$代入计算程序,得$(-3)×4 - (-1) = -12 + 1 = -11$,因为$-11 < -5$,所以输出结果。最后输出的结果是$-11$。
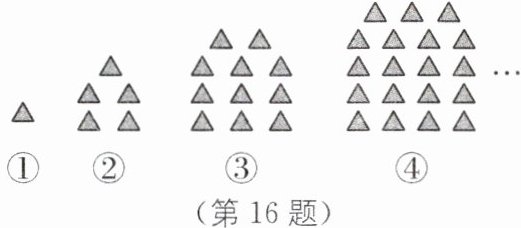
16. 下面各图形是由大小相同的三角形摆放而成的,第1个图形有1个三角形,第2个图形有5个三角形,第3个图形有11个三角形,第4个图形有19个三角形,…,依此规律,则第n个图形中三角形个数是______.
$n^{2}+n-1$
答案:$n^{2}+n-1$[解析]观察题图中三角形的个数与图形的序号的关系,有如下规律:第1个图形:$1^{2}+0$;第2个图形:$2^{2}+1;$第3个图形:$3^{2}+2$;第4个图形:$4^{2}+3$;……;则第n个图形:$n^{2}+n-1.$
解析:
第1个图形:$1=1^{2}+(1-1)$
第2个图形:$5=2^{2}+(2-1)$
第3个图形:$11=3^{2}+(3-1)$
第4个图形:$19=4^{2}+(4-1)$
……
第n个图形:$n^{2}+(n-1)=n^{2}+n-1$
$n^{2}+n-1$
17. 已知$A= 2x^{2}+ax-7$,$B= bx^{2}-\frac{3}{2}x-\frac{5}{2}$.当$A-2B$的值与x无关时,$a+b= $
-2
.
答案:-2 [解析]$A-2B=(2x^{2}+ax-7)-2(bx^{2}-\frac{3}{2}x-\frac{5}{2})=2x^{2}+ax-7-2bx^{2}+3x+5=(2-2b)x^{2}+(a+3)x-2.$
∵A-2B的值与x无关,
∴$2-2b=0,a+3=0,$
∴$a=-3,b=1.\therefore a+b=-3+1=-2.$
18. 已知a,b,c,d表示4个不同的正整数,满足$a+b^{2}+c^{3}+d^{4}= 90$,其中$d>1$,则$a+b+c+d$的最大值是______
70
.
答案:70 [解析]要使$a+b+c+d$取最大值,b,c,d尽可能取最小值,
∴$d=2,c=1,b=3,a=90-(b^{2}+c^{3}+d^{4})=90-(3^{2}+1^{3}+2^{4})=64,$
∴$a+b+c+d$的最大值为$64+3+1+2=70.$
19.(2025·常州武进区翠竹中学期中)先化简,再求值:$5(3a^{2}b-ab^{2})-3(-ab^{2}-3a^{2}b)$,其中$a= -1$,$b= \frac{1}{2}$.
答案:原式$=15a^{2}b-5ab^{2}+3ab^{2}+9a^{2}b=24a^{2}b-2ab^{2},$当$a=-1,b=\frac{1}{2}$时,原式$=24×(-1)^{2}×\frac{1}{2}-2×(-1)×(\frac{1}{2})^{2}=\frac{25}{2}.$
解析:
原式$=15a^{2}b - 5ab^{2} + 3ab^{2} + 9a^{2}b$
$=(15a^{2}b + 9a^{2}b) + (-5ab^{2} + 3ab^{2})$
$=24a^{2}b - 2ab^{2}$
当$a = -1$,$b = \frac{1}{2}$时,
原式$=24×(-1)^{2}×\frac{1}{2} - 2×(-1)×(\frac{1}{2})^{2}$
$=24×1×\frac{1}{2} - 2×(-1)×\frac{1}{4}$
$=12 + \frac{1}{2}$
$=\frac{25}{2}$
20.(2025·镇江期末)[阅读]同学们,我们知道数可以比较大小,比如$3>2$,那么两个代数式可以比较大小吗?例如:比较$3x+5与3x+3$的大小,我们可以这样做:因为$(3x+5)-(3x+3)= 3x+5-3x-3= 2>0$,所以$3x+5>3x+3$.[尝试]比较代数式$3a^{2}+10a+3与2a^{2}+10a+1$的大小,说明理由.
答案:$3a^{2}+10a+3>2a^{2}+10a+1$.理由如下:$(3a^{2}+10a+3)-(2a^{2}+10a+1)=3a^{2}+10a+3-2a^{2}-10a-1=a^{2}+2\geq 2,$
∴$3a^{2}+10a+3>2a^{2}+10a+1.$
21. 如图,在一块长为$2x$m、宽为y m$(2x>y)$的长方形铁皮的四个角上,分别截去半径为$\frac{y}{2}$m的四分之一圆.
(1)求剩余铁皮的面积(即阴影部分的面积).
(2)当$x= 6$,$y= 8$时,剩余铁皮的面积是多少?(π取3.14)

答案:
(1)由已知,得剩余铁皮的面积=长方形铁皮面积-截去半径为$\frac{y}{2}m$的圆的面积$×\frac{1}{4}×4=2xy-\pi ×\frac{y^{2}}{4}×\frac{1}{4}×4=(2xy-\frac{\pi y^{2}}{4})m^{2}.$故剩余铁皮的面积是$(2xy-\frac{\pi y^{2}}{4})m^{2}.$
(2)当$x=6,y=8$时,剩余铁皮的面积为$2xy-\frac{\pi y^{2}}{4}\approx 2×6×8-50.24=45.76(m^{2}).$故剩余铁皮的面积是$45.76m^{2}.$