1.(2024·台湾中考)有研究报告指出,1880年至2020年全球平均气温上升趋势约为每十年上升0.08℃.已知2020年全球平均气温为14.88℃,假设未来的全球平均气温上升趋势与上述趋势相同,且每年上升的度数相同,则预估2020年之后第x年的全球平均气温为多少℃?(
B
).
A.14.88+0.08x
B.14.88+0.008x
C.14.88+0.08[x+(2020-1880)]
D.14.88+0.008[x+(2020-1880)]
答案:B
解析:
每十年上升$0.08^\circC$,则每年上升$0.08÷10 = 0.008^\circC$。
2020年之后第$x$年,气温上升了$0.008x^\circC$。
2020年全球平均气温为$14.88^\circC$,故预估气温为$14.88 + 0.008x$。
B
2. 在代数式$x^{2}+5$,0,$\frac{2}{x+1}$,y,-2,-3x+2中,整式有(
A
).
A.5个
B.4个
C.3个
D.2个
答案:A
解析:
整式有$x^{2}+5$,0,y,-2,-3x+2,共5个。
A
3. 若$-2a^{m}b^{4}与5a^{2m+n}b^{n+2}$可以合并成一项,则$m^{n}$的值是(
A
).
A.4
B.0
C.-1
D.1
答案:A
解析:
因为$-2a^{m}b^{4}$与$5a^{2m+n}b^{n+2}$可以合并成一项,所以它们是同类项。
同类项要求相同字母的指数分别相等,可得:
$\begin{cases}m = 2m + n \\ 4 = n + 2\end{cases}$
由$4 = n + 2$,解得$n = 2$。
将$n = 2$代入$m = 2m + n$,得$m = 2m + 2$,解得$m=-2$。
则$m^{n}=(-2)^{2}=4$。
A
4. 下列合并同类项正确的是(
D
).
A.$2x+4x= 8x^{2}$
B.$3x+2y= 5xy$
C.$7x^{2}-3x^{2}= 4$
D.$9a^{2}b-9ba^{2}= 0$
答案:D
解析:
A. $2x + 4x = 6x$,故A错误;
B. $3x$与$2y$不是同类项,不能合并,故B错误;
C. $7x^2 - 3x^2 = 4x^2$,故C错误;
D. $9a^2b - 9ba^2 = 0$,故D正确。
D
5.(2025·扬州邗江区期末)九月开学季,书店开展优惠活动,某套名著原价为m元,现售价为$(0.7m-10)$元,则下列说法符合题意的是(
B
).
A.原价减10元后再打7折
B.原价打7折后再减10元
C.原价打3折后再减10元
D.原价减10元后再打3折
答案:B
6. 下列结论中正确的是(
D
).
A.单项式$\frac{\pi xy^{2}}{4}的系数是\frac{1}{4}$,次数是4
B.单项式m的次数是1,没有系数
C.多项式$2x^{2}+xy^{2}+3$是二次多项式
D.在$\frac{1}{x}$,$2x+y$,$-a^{2}b$,$\frac{x-y}{\pi}$,0中,整式有4个
答案:D [解析]A.单项式$\frac{\pi xy^{2}}{4}$的系数是$\frac{\pi}{4}$,次数是3,故该选项不符合题意;B.单项式m的次数是1,系数是1,故该选项不符合题意;C.多项式$2x^{2}+xy^{2}+3$是三次多项式,故该选项不符合题意;D.在$\frac{1}{x},2x+y,-a^{2}b,\frac{x-y}{\pi},0$中,整式有4个,故该选项符合题意.故选D.
7.(2024·河北模拟)如图,已知圆环内直径为a厘米,外直径为b厘米,将9个这样的圆环一个接一个环套地连成一条锁链,那么这条锁链拉直后的长度为(
A
).
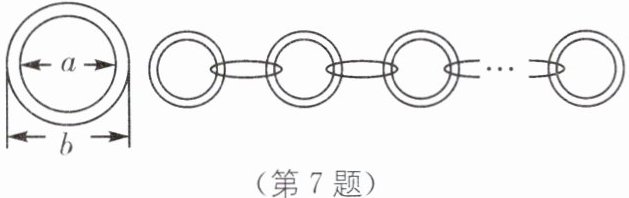
A.$(8a+b)$厘米
B.$(8b+a)$厘米
C.$(9a-b)$厘米
D.$(9b-a)$厘米
答案:A
解析:
一个圆环长度为外直径$b$厘米,每增加一个圆环,重叠部分为内直径$a$厘米。9个圆环连成锁链,有8个重叠部分。拉直后的长度为:$9b - 8(b - a) = 8a + b$。
A
8. 现有一列数$a_{1},a_{2},a_{3},…,a_{98},a_{99},a_{100}$,其中$a_{3}= 2024$,$a_{7}= -2023$,$a_{98}= -2$,且满足任意相邻三个数的和为同一个常数,则$a_{1}+a_{2}+a_{3}+…+a_{98}+a_{99}+a_{100}$的值为(
B
).
A.2056
B.-2056
C.2025
D.-2025
答案:B [解析]
∵任意相邻三个数的和为同一个常数,
∴$a_{1}+a_{2}+a_{3}=a_{2}+a_{3}+a_{4},a_{2}+a_{3}+a_{4}=a_{3}+a_{4}+a_{5},$$a_{3}+a_{4}+a_{5}=a_{4}+a_{5}+a_{6}.$$\therefore a_{1}=a_{4},a_{2}=a_{5},a_{3}=a_{6}.$
∴该数列为3个数为一个循环的一组循环数.$\because a_{7}=-2023,a_{98}=-2,7÷3=2\cdots \cdots 1,$$98÷3=32\cdots \cdots 2,$$\therefore a_{1}=-2023,a_{2}=-2.$$\therefore a_{1}+a_{2}+a_{3}=-2023+(-2)+2024=-1.$$\because 100÷3=33\cdots \cdots 1.\therefore a_{100}=a_{1}=-2023.$$\therefore a_{1}+a_{2}+a_{3}+\cdots +a_{98}+a_{99}+a_{100}=(a_{1}+a_{2}+a_{3})+\cdots +(a_{97}+a_{98}+a_{99})+a_{100}=-1×33+(-2023)=-2056.$故选B.
9.(2024·南京雨花台区模拟)化简$2m-(3m+8m)$的结果是
-9m
.
答案:-9m [解析]原式$=2m-3m-8m=-9m.$
解析:
$2m-(3m+8m)=2m-3m-8m=-9m$
10.(2025·扬州期末)已知a,b,c在数轴上的位置如图所示,其中$|a|<|c|$,化简:$|b-c|-|a+c|+2|b-a|= $
3a-b
.
答案:3a-b
解析:
由数轴知:$c < b < 0 < a$,且$|a| < |c|$
$\because c < b$
$\therefore b - c > 0$
$\because |a| < |c|$,$a > 0$,$c < 0$
$\therefore a + c < 0$
$\because b < 0 < a$
$\therefore b - a < 0$
$|b - c| - |a + c| + 2|b - a|$
$= (b - c) - [-(a + c)] + 2[-(b - a)]$
$= b - c + a + c - 2b + 2a$
$= 3a - b$
$3a - b$
11. 研究下列算式你会发现有什么规律:$4×1×2+1= 3^{2}$;$4×2×3+1= 5^{2}$;$4×3×4+1= 7^{2}$;$4×4×5+1= 9^{2}$;…请你将找出的规律用含一个字母的等式表示出来:
$4n(n+1)+1=(2n+1)^{2}$
.
答案:$4n(n+1)+1=(2n+1)^{2}$
12. 赋予“2a”一个实际意义为
若梨的价格是2元/千克,则2a表示买a千克梨的金额(答案不唯一)
.
答案:若梨的价格是2元/千克,则2a表示买a千克梨的金额(答案不唯一)
解析:
若苹果的单价是2元/个,则2a表示购买a个苹果的总价(答案不唯一)
13. 按如图所示的程序计算,若开始输入的值为$x= 3$,则最后输出的结果为
156
.
答案:156 [解析]第1次输入$x=3$,则$x(x+1)=12<100$,第2次输入$x=12$,则$x(x+1)=156>100.$
解析:
第1次输入$x = 3$,计算$x(x + 1)=3×(3 + 1)=12$,$12<100$;第2次输入$x = 12$,计算$x(x + 1)=12×(12 + 1)=156$,$156>100$,输出结果。
156