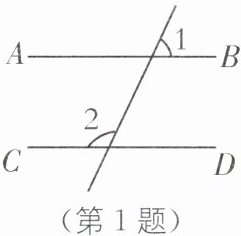
1.(2024·重庆中考)如图,AB// CD,$\angle 1= 65^\circ,则\angle 2的度数是(
B
).A. 105^\circ B. 115^\circ C. 125^\circ D. 135^\circ$
答案:B
解析:
因为 $AB // CD$,所以$\angle 1$的对顶角与$\angle 2$互补。
$\angle 1$的对顶角等于$\angle 1 = 65^\circ$,
则$\angle 2=180^\circ - 65^\circ = 115^\circ$。
B
2. 跨学科 光的折射 (2024·达州中考)当光线从空气射入水中时,光线的传播方向发生了改变,这就是光的折射现象(如图所示),图中$\angle 1= 80^\circ,$$\angle 2= 40^\circ,则\angle 3的度数为(
B
).A. 30^\circ B. 40^\circ C. 50^\circ D. 70^\circ$

答案:B
解析:
由光的折射规律,法线与水面垂直,设水面为直线$l$,法线为直线$m$,则$l\perp m$,$\angle 1$与入射角互余,$\angle 2$与折射角互余。
入射角$=90^\circ - \angle 1=90^\circ - 80^\circ=10^\circ$,折射角$=90^\circ - \angle 2=90^\circ - 40^\circ=50^\circ$。
由图可知$\angle 3=$折射角$-$入射角$=50^\circ - 10^\circ=40^\circ$。
B
3.(2024·福建中考)在同一平面内,将直尺、含$30^\circ角的三角尺和木工角尺(CD\perp DE)$按如图方式摆放,若AB// CD,则$\angle 1的大小为( ).A. 30^\circ B. 45^\circ C. 60^\circ D. 75^\circ$

答案:3.A [解析]如图,

∵AB//CD,
∴∠CDB=∠ABF=60°.
∵CD⊥DE,
∴∠CDE=90°,
∴∠1=180°−60°−90°=30°. 故选A
4.(2024·宿迁泗洪期中)如图,AB// CD,$\angle CED= 90^\circ,$$\angle BED= 30^\circ,求\angle C$的度数.

答案:
∵∠BED=30°,∠CED=90°,
∴∠AEC=180°−90°−30°=60°.
∵AB//CD,
∴∠C=∠AEC=60°. 两直线平行,内错角相等
5.(2024·盐城中考)小明将一块直角三角板摆放在直尺上,如图,若$\angle 1= 55^\circ,则\angle 2的度数为(
B
).A. 25^\circ B. 35^\circ C. 45^\circ D. 55^\circ$

答案:B
解析:
∵直尺两边平行,
∴∠1的同位角等于∠1=55°,
∵直角三角板的直角为90°,
∴∠2=90°-55°=35°,
B
6.(2025·常州期末)将一块含$30^\circ$角的直角三角板与一把直尺按如图所示方式摆放,$\angle C= 90^\circ,$$\angle A= 30^\circ.若\angle 1= \alpha^\circ,则\angle 3-\angle 2的大小为(
D
).A. 30^\circ B. 60^\circ C. (30+\alpha)^\circ D. (30+2\alpha)^\circ$
答案:D
解析:
设直尺上下两边分别为直线$l_1$、$l_2$,且$l_1// l_2$。
记$AB$与$l_2$交于点$D$,$BC$与$l_1$交于点$E$。
因为$l_1// l_2$,所以$\angle 3=\angle ADE$(内错角相等)。
在$\triangle BDE$中,$\angle ADE=\angle 2+\angle BED$(外角性质)。
又$\angle BED=\angle 1=\alpha^\circ$(对顶角相等),故$\angle 3=\angle 2+\alpha^\circ$,即$\angle 3-\angle 2=\alpha^\circ$。
在$\triangle ABC$中,$\angle A=30^\circ$,$\angle C=90^\circ$,则$\angle ABC=60^\circ$。
因为$l_1// l_2$,$\angle 1+\angle ABC+\angle 2=180^\circ$(同旁内角互补),即$\alpha^\circ+60^\circ+\angle 2=180^\circ$,解得$\angle 2=120^\circ-\alpha^\circ$。
由$\angle 3=\angle 2+\alpha^\circ$,得$\angle 3=120^\circ$,故$\angle 3-\angle 2=120^\circ-(120^\circ-\alpha^\circ)=\alpha^\circ$。
综上,$\angle 3-\angle 2=(30+2\alpha)^\circ$。
D
7.(2024·湖北黄石黄石港区期末)如图,在$\triangle ABC$中,BE,CE,CD分别平分$\angle ABC,$$\angle ACB,$$\angle ACF,$AB// CD,下列结论:$①\angle A= \angle ABC;$$②\angle BEC= 90^\circ+\angle ABD;$$③\angle A= \angle D;$$④2\angle BEC-\angle A= 180^\circ,$其中所有正确结论的序号是(
C
).
A.①②
B.③④
C.①②④
D.①②③④
答案:7.C [解析]
∵CD平分∠ACF,
∴∠ACD=∠DCF.
∵AB//CD,
∴∠A=∠ACD,∠ABC=∠DCF,
∴∠A=∠ABC,故①正确;
∵BE,CE分别平分∠ABC,∠ACB,
∴∠ABE=∠EBC=$\frac{1}{2}$∠ABC,∠ACE=∠BCE=$\frac{1}{2}$∠ACB,
∴∠BEC=180°−(∠EBC+∠ECB)=180°−($\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB)=180°−$\frac{1}{2}$(∠ABC+∠ACB)=180°−$\frac{1}{2}$(180°−∠A)=180°−90°+$\frac{1}{2}$∠A=90°+$\frac{1}{2}$∠A,
∴2∠BEC=180°+∠A,
∴2∠BEC−∠A=180°,故④正确;
∵∠A=∠ABC,
∴∠ABD=$\frac{1}{2}$∠A,
∴∠BEC=90°+∠ABD,故②正确;
∵AB//CD,
∴∠ABD=∠D,
∴∠D=$\frac{1}{2}$∠A,故③不正确综上所述,其中正确结论的序号是①②④. 故选C.
8. 跨学科 光的折射 (2024·盐城一模)光从空气斜射入水中,传播方向会发生变化.如图,表示水面的直线AB与表示水底的直线CD平行,光线EF从空气射入水中,改变方向后射到水底G处,FH是EF的延长线,若$\angle 1= 43^\circ,$$\angle 2= 15^\circ,则\angle CGF$的度数是______.

58°
答案:58° [解析]
∵∠1=43°,∠2=15°,
∴∠AFG=180°−∠1−∠2=180°−43°−15°=122°.
∵AB//CD,
∴∠CGF=180°−∠AFG=180°−122°=58°.