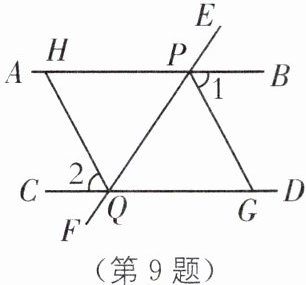
9. (2025·内蒙古包头昆都仑区期末)如图,直线$EF分别与直线AB$,$CD相交于点P和点Q$,$PG平分\angle BPQ$,$QH平分\angle CQP$,并且$\angle 1= \angle 2$. 说出图中哪些直线互相平行,并说明理由.
答案:AB//CD,QH//PG.理由如下:
∵PG平分∠BPQ,QH平分∠CQP,
∴∠GPQ=∠1=$\frac{1}{2}$∠BPQ,∠HQP=∠2=$\frac{1}{2}$∠CQP.
∵∠1=∠2,
∴∠GPQ=∠HQP,∠BPQ=∠CQP,
∴QH//PG,AB//CD.
10. 如图,已知$AD \perp BC$,$EF \perp BC$,$\angle 1= \angle 2$. 试说明$DG // BA$.

答案:
∵AD⊥BC,EF⊥BC,
∴∠EFB=∠ADB=90°,
∴AD//EF,
∴∠1=∠BAD.
∵∠1=∠2,
∴∠2=∠BAD,
∴DG//AB.
11. 共顶点模型 (2025·河南郑州中牟期末改编)[综合与实践]学习完《平行线的判定》,我们积累了一定的研究经验,小凯和小芳将一副透明三角板中的两个直角三角尺的直角顶点$C$按如图所示的方式叠放在一起,其中$\angle A= \angle B= 45^{\circ}$,$\angle D= 30^{\circ}$,$\angle E= 60^{\circ}$.
(1)[操作判断]若$\angle DCB = 55^{\circ}$,则$\angle ACE= $
125°
;若$\angle ACE= 158^{\circ}$,则$\angle DCB= $
22°
;
(2)[性质探究]由(1)猜想$\angle ACE与\angle DCB$的数量关系,并证明你的猜想;
猜想:∠ACE+∠DCB=180°.理由如下:∵∠ACD=90°−∠DCB,∠BCE=90°−∠DCB,∴∠ACE=∠ACD+∠BCE+∠DCB =90°−∠DCB+90°−∠DCB+∠DCB =180°−∠DCB,即∠ACE+∠DCB=180°.
(3)[拓展应用]当$\angle BCE<180^{\circ}且点B在直线CE$的上方时,这两个三角尺存在一组边互相平行,请直接写出$\angle BCE$所有可能的度数(不必说明理由).
30°,45°,120°,135°,165°

答案:
(1)125° 22° [解析]
∵∠DCB=55°,∠ACB=90°,
∴∠ACD=35°.
∵∠DCE=90°,
∴∠ACE=90°+35°=125°.
∵∠ACE=158°,
∴∠ACD=∠ACE−90°=158°−90°=68°,
∴∠DCB=90°−68°=22°.
(2)猜想:∠ACE+∠DCB=180°.理由如下:
∵∠ACD=90°−∠DCB,∠BCE=90°−∠DCB,
∴∠ACE=∠ACD+∠BCE+∠DCB =90°−∠DCB+90°−∠DCB+∠DCB =180°−∠DCB,即∠ACE+∠DCB=180°.
(3)存在,30°,45°,120°,135°,165°.
理由:当CB//DE时,∠BCE=120°;
当AC//DE时,∠BCE=30°;
当AB//DE时,∠BCE=165°;
当AB//CD时,∠BCE=135°;
当AB//CE时,∠BCE=45°.