2025年实验班提优训练七年级数学上册苏科版第135页解析答案

10.(2024·宿迁沭阳期中)如图,在△ABC 中,∠B= ∠C,点 D,E 分别在 AB,AC 上,且∠ADE= ∠AED.DE 与 BC 平行吗？为什么？

答案：平行.理由如下:
∵在△ABC中,∠B=∠C,
∴∠B=∠C=$\frac{180^\circ-\angle A}{2}$.
∵∠ADE=∠AED,
∴∠ADE=∠AED=$\frac{180^\circ-\angle A}{2}$,
∴∠B=∠ADE,
∴DE//BC.

11. 将△ABC 纸片沿 DE 折叠,其中∠B= ∠C.
(1)如图(1),点 C 落在 BC 边上的点 F 处,AB 与 DF 是否平行？请说明理由.
(2)如图(2),点 C 落在四边形 ABED 内部的点 G 处,探索∠B 与∠1+∠2 之间的数量关系,并说明理由.

答案：

(1)AB与DF平行.理由如下:由翻折,得∠DFC=∠C.又∠B=∠C,
∴∠B=∠DFC,
∴AB//DF.
(2)连接GC,如图所示.由翻折,得∠DGE=∠ACB.
∵∠1=180°−∠CDG=180°−(180°−∠DGC−∠DCG)=∠DGC+∠DCG,∠2=180°−∠GEC=180°−(180°−∠CGE−∠GCE)=∠EGC+∠ECG,
∴∠1+∠2=∠DGC+∠DCG+∠EGC+∠ECG=(∠DGC+∠EGC)+(∠DCG+∠ECG)=∠DGE+∠DCE=2∠ACB.
∵∠B=∠ACB,
∴∠1+∠2=2∠B.

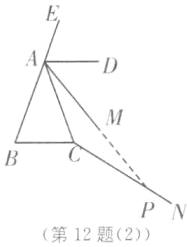
12. 分类讨论思想如图,已知∠ABC= 70°,∠BAC= 40°,AD 平分∠CAE.
(1)求证：AD//BC；
(2)若射线 AD 绕点 A 以每秒 1°的速度顺时针方向旋转得到 AM,同时,射线 CA 绕点 C 以每秒 2°的速度顺时针方向旋转得到 CN,AM 和 CN 交于点 P,设旋转时间为 t 秒.
①当 0＜t＜55 时,请写出∠APC 与∠BAP 之间的数量关系,并说明理由；
②当 0＜t＜70 时,若1/5∠APC+∠BCP= 180°,请直接写出 t 的值.

精题详解

答案：

(1)
∵∠BAC=40°,
∴∠CAE=180°−∠BAC=140°.
∵AD平分∠CAE,
∴∠DAE=$\frac{1}{2}$∠CAE=70°.
∵∠ABC=70°,
∴∠ABC=∠DAE,
∴AD//BC.
(2)①
∵∠DAE=∠DAC=70°,射线AD绕点A以每秒1°的速度顺时针方向旋转得到AM,
∴∠CAM=70°−t.
∵∠BAC=40°,
∴∠BAP=∠BAC+∠CAM=40°+(70°−t)=110°−t.
∵射线CA绕点C以每秒2°的速度顺时针方向旋转得到CN,
∴∠ACP=2t,
∴∠APC=180°−∠CAM−∠ACP=180°−(70°−t)−2t=110°−t,
∴∠APC=∠BAP.
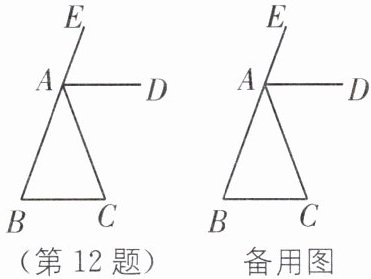
②当0＜t＜55时,如图
(1).
由①,可得∠APC=110°−t,∠ACP=2t,
∴∠BCP=70°+2t.
∵$\frac{1}{5}$∠APC+∠BCP=180°,
∴$\frac{1}{5}$(110°−t)+70°+2t=180°,解得t=$\frac{440}{9}$;
当55≤t＜70时,如图
(2).
∵∠ACP=2t,∠ACB=70°,
∴∠BCP=360°−∠ACB−∠ACP=360°−70°−2t=290°−2t.
∵∠APC=110°−t,$\frac{1}{5}$∠APC+∠BCP=180°,
∴$\frac{1}{5}$(110°−t)+(290°−2t)=180°,解得t=60.
综上,t的值为60或$\frac{440}{9}$.