1. (2025·遵化一模)如图,用同样大小的三角板比较∠A 和∠B 的大小,下列判断正确的是(
B
).
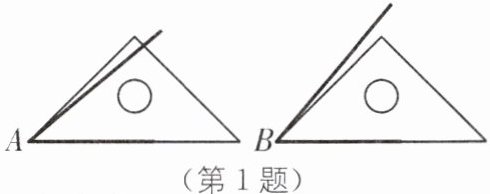
A.∠A>∠B
B.∠A<∠B
C.∠A= ∠B
D.没有量角器,无法确定
答案:B
2. (2025·河北保定安新期末)如图,将一副直角三角板的顶点重合后放置,则∠AOC 与∠DOB 的大小关系是(
B
).

A.∠AOC>∠DOB
B.∠AOC= ∠DOB
C.∠AOC<∠DOB
D.不能确定
答案:B
解析:
∠AOC=∠AOB+∠BOC,∠DOB=∠DOC+∠BOC,
因为∠AOB=∠DOC=90°,
所以∠AOC=∠DOB。
B
3. (2025·淮安期末)如图所示的正方形网格中,点 A,B,C 是格点,则∠B ______ 2∠C.(填“>”“<”或“=”)

答案:> [解析]连接BD,如图.

由题意可得,∠C=∠DBE=∠BDE=45°,
∵在△DBC中,∠DBC=180°−∠C−∠BDE=90°,
∴∠ABC=∠ABD+∠DBC>2∠C=90°,
∴∠ABC>2∠C.
4. (教材 P168 例 4·变式)如图,∠ABC= 110°,∠DBE= 50°,∠CBD= ∠ABE,BF 平分∠ABE.
(1)求∠ABF 的度数.
(2)∠CBE= ∠ABD 吗?为什么?

答案:
(1)
∵∠ABC=110°,∠DBE=50°,
∴∠CBD+∠ABE=110°−50°=60°.
又∠CBD=∠ABE,
∴∠CBD=∠ABE=$\frac{1}{2}$×60°=30°.
∵BF平分∠ABE,
∴∠ABF=∠EBF=$\frac{1}{2}$∠ABE=$\frac{1}{2}$×30°=15°.
由角平分线的性质可得
(2)∠CBE=∠ABD.理由如下:
∵∠CBD=∠ABE,
∴∠CBD+∠DBE=∠ABE+∠DBE,
即∠CBE=∠ABD.
5. (2025·河北廊坊霸州期末)若∠A= 20°20′,∠B= 20°15′30″,∠C= 20.35°,则(
D
).
A.∠A>∠B>∠C
B.∠B>∠A>∠C
C.∠A>∠C>∠B
D.∠C>∠A>∠B
答案:D [解析]
∵∠C=20.35°=20°+0.35°,0.35°=0.35×60'=21′,
∴∠C=20°21'.
∵∠A=20°20',∠B=20°15′30",
∴∠C>∠A>∠B.故选D
6. (2025·无锡期末)如图,∠AOB 是直角,∠AOC= 50°,射线 OP 从边 OA 出发,绕点 O 逆时针旋转直至与边 OB 重合,在旋转过程中,下列情形不可能出现的是(
D
).
A.OP 平分∠AOC
B.OP 平分∠AOB
C.OC 平分∠BOP
D.OC 平分∠AOP
答案:D [解析]当射线OP旋转到∠AOP=∠POC时,
则OP平分∠AOC,故A选项可能出现,不符合题意;
当射线OP旋转到∠AOP=∠POB时,
则OP平分∠AOB,故B选项可能出现,不符合题意;
当射线OP旋转到∠BOC=∠POC时,
则OC平分∠BOP,故C选项可能出现,不符合题意;
∵∠AOC=50°,若∠AOC=∠POC,则∠POC=50°,
∴∠AOP=100°.
但∠AOB是直角,为90°,且射线OP从边OA出发,绕点O逆时针旋转直至与边OB重合,故在∠AOB中不可能有一个大于90°的∠AOP.故D选项不可能出现,符合题意.故选D.
7. 如图,点 O 在直线 AB 上,OD 是∠BOC 的平分线,若∠AOC= 140°,则∠BOD 的度数为 ______.

20°
答案:20°
解析:
∵点 O 在直线 AB 上,∠AOC = 140°,
∴∠BOC = 180° - ∠AOC = 180° - 140° = 40°。
∵OD 是∠BOC 的平分线,
∴∠BOD = $\frac{1}{2}$∠BOC = $\frac{1}{2}$×40° = 20°。
20°
8. 方程思想 如图,OC 是∠AOB 的平分线,∠COD= 20°.
(1)若∠AOD= 30°,求∠AOB 的度数;
(2)若∠BOD= 2∠AOD,求∠AOB 的度数.

答案:
(1)
∵∠COD=20°,∠AOD=30°,
∴∠AOC=∠COD+∠AOD=20°+30°=50°.
∵OC是∠AOB的平分线,
∴∠AOB=2∠AOC=100°.
(2)设∠AOD=x,则∠BOD=2x,
∴∠AOB=∠AOD+∠BOD=3x.
∵OC是∠AOB的平分线,
∴∠AOC=$\frac{1}{2}$∠AOB=$\frac{3}{2}$x,
∴$\frac{3}{2}$x−x=20°,解得x=40°,
由∠COD=20°,可建立方程
∴∠AOB=3x=120°.
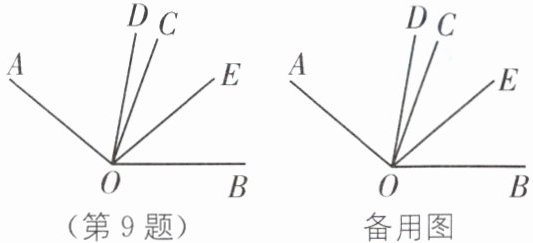
9. (2024·重庆一中期末)如图,∠AOB 为钝角,射线 OC 平分∠AOB,射线 OD 在∠AOC 内部,射线 OE 平分∠BOD.
(1)若∠COD= 10°,∠AOB= 140°. 求∠COE 的度数;
(2)请写出∠AOD 与∠COE 度数之间的等量关系,并说明理由.
答案:
(1)
∵OC平分∠AOB,∠AOB=140°,
∴∠BOC=$\frac{1}{2}$∠AOB=70°,
∵∠COD=10°,
∴∠BOD=∠BOC+∠COD=80°.
∵OE平分∠BOD,
∴∠DOE=$\frac{1}{2}$∠BOD=40°,
∴∠COE=∠DOE−∠COD=40°−10°=30°.
(2)∠AOD=2∠COE.理由如下:
∵OC平分∠AOB,
∴∠AOC=∠BOC=$\frac{1}{2}$∠AOB.
∵∠COD+∠AOD=∠AOC,
∴∠AOB=2∠AOC=2(∠COD+∠AOD).
∵OE平分∠BOD,
∴∠DOE=∠BOE=$\frac{1}{2}$∠BOD.
∵∠COE+∠COD=∠DOE,
∴∠BOD=2∠DOE=2(∠COE+∠COD).
∵∠AOB−∠BOD=∠AOD,
∴2∠COD+2∠AOD−2∠COE−2∠COD=∠AOD,
∴∠AOD=2∠COE.