1. (教材 P166 练习 T3·变式)(2024·安徽亳州蒙城期末)如果∠1 与∠2 互补,∠2 与∠3 互余,那么∠1 与∠3 的关系是(
C
).
A.∠1= ∠3
B.∠1= 180°-∠3
C.∠1= 90°+∠3
D.∠3= 90°+∠1
答案:C
解析:
∵∠1与∠2互补,
∴∠1 + ∠2 = 180°,则∠2 = 180° - ∠1。
∵∠2与∠3互余,
∴∠2 + ∠3 = 90°。
将∠2 = 180° - ∠1代入∠2 + ∠3 = 90°,得180° - ∠1 + ∠3 = 90°,
移项可得∠1 = 180° - 90° + ∠3 = 90° + ∠3。
C
2. (2025·福建泉州期末)如图,∠AOB 的大小可由量角器测得,则∠AOB 的补角的大小为(
B
).
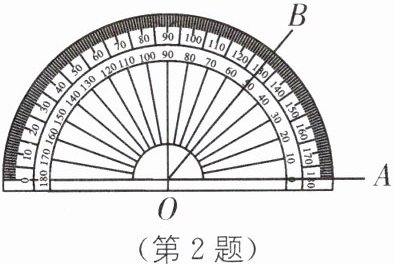
A.140°
B.130°
C.50°
D.40°
答案:B[解析]由量角器可知,∠AOB=50°,
∴∠AOB的补角的大小为130°.故选B.
3. (2025·福建龙岩期末改编)如图,点 O 为直线 AB 上一点,∠AOC= ∠BOC,∠DOE= 90°,则图中互余的角有(
A
).

A.4 对
B.3 对
C.2 对
D.1 对
答案:A [解析]
∵点O为直线AB上一点,
∴∠AOC=∠BOC=90°,
∴∠AOC=∠AOD+∠DOC=90°,∠BOC=∠BOE+∠COE=90°.
∵∠DOE=90°,
∴∠DOE=∠DOC+∠COE=90°,∠AOD+∠BOE=90°,
∴图中互余的角有∠AOD和∠DOC,∠BOE和∠COE,∠DOC和∠COE,∠AOD和∠BOE,共4对.故选A 归纳总结 本题主要考查了余角的定义,根据和为90度的两个角互为余角即可求解.
4. (2025·山东德州禹城期末)已知一个角的补角比这个角的余角 3 倍大 10°,则这个角的度数是
50
°.
答案:50
解析:
设这个角的度数是$x$°,则它的补角为$(180 - x)$°,余角为$(90 - x)$°。
根据题意可得:$180 - x = 3(90 - x) + 10$
$180 - x = 270 - 3x + 10$
$-x + 3x = 270 + 10 - 180$
$2x = 100$
$x = 50$
50
5. 方程思想 如图,已知∠1:∠2:∠3:∠4= 1:2:3:4,求∠1,∠2,∠3,∠4 的度数.

答案:设∠1=x,则∠2=2x,∠3=3x,∠4=4x,
∴x+2x+3x+4x=360°,
∴x=36°,
∴∠1=36°,∠2=72°,∠3=108°,∠4=144°.
6. (2025·广东广州期末)一副三角板按如图的方式摆放,则∠BAD 的补角的度数是(
D
).

A.15°
B.75°
C.135°
D.165°
答案:D[解析]
∵∠EAD=45°,∠CAB=30°,
∴∠BAD=∠EAD−∠CAB=15°,
∴∠BAD的补角的度数是180°−∠BAD=165°.故选D.思路引导 本题考查了三角形板中的角度计算、补角,熟练掌握补角的定义是解题关键,先利用角的和差可得∠BAD=15°,然后利用补角的定义求解即可.
7. (2025·湖北十堰郧西期末)如图,∠AOB= ∠COD= ∠EOF= 90°,则∠1,∠2,∠3 之间的数量关系为(
D
).
A.∠1+∠2+∠3= 90°
B.∠1+∠2-∠3= 90°
C.∠2+∠3-∠1= 90°
D.∠1-∠2+∠3= 90°
答案:D[解析]
∵∠3+∠BOC=∠DOB+∠BOC=90°,
∴∠3=∠BOD.
∵∠EOD+∠1=90°,
∴∠BOD−∠2+∠1=90°,
∴∠3−∠2+∠1=90°.故选D.
8. (2025·盐城东台期末改编)将一副三角尺按下列位置摆放,使∠α 和∠β 互余的摆放方式是(
A
).

答案:A[解析]A.∠α与∠β互余,故本选项正确;B.∠α=∠β,故本选项错误;C.∠α=∠β,故本选项错误;D.∠α与∠β互补,故本选项错误.故选A.
9. (重庆沙坪坝区自主招生)如图,∠AOB= ∠COD= 90°,∠AOD= 110°,则∠BOC 的度数是(
C
).

A.20°
B.65°
C.70°
D.75°
答案:C[解析]由题意知,∠BOD=∠AOD−∠AOB=110°−90°=20°,
∴∠BOC=∠COD−∠BOD=70°.故选C.