10. 如图,已知线段 $AC= 12\ cm$,点 B 在线段 AC 上,满足 $BC= \frac{1}{2}AB$.
(1)求 AB 的长;
(2)若点 D 是 AB 的中点,点 E 是 AC 的中点,求线段 DE 的长.
]
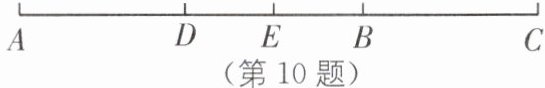
答案:
(1)
∵BC=$\frac{1}{2}$AB,AC=12cm,
∴BC=$\frac{1}{3}$AC=4cm,
∴AB=AC−BC=12−4=8(cm).
(2)
∵点D是AB的中点,AB=8cm,
∴AD=$\frac{1}{2}$AB=4cm.
∵点E是AC的中点,AC=12cm,
∴AE=$\frac{1}{2}$AC=6cm,
∴DE=AE−AD=6−4=2(cm).
归纳总结 本题考查两点间的距离、线段的和、差及倍数关系等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
11. 数形结合思想 (2025·福建厦门思明区期末)如图,C 是线段 AB 的中点.
(1)若点 D 在线段 CB 上,且 $DB= 1.5\ cm$,$AD= 6.5\ cm$,求线段 CD 的长度;
(2)若将(1)中的“点 D 在线段 CB 上”改为“点 D 在 CB 的延长线上”,其他条件不变,请画出相应的示意图,并求出此时线段 CD 的长度.
]

答案:(1)AB=AD+BD=6.5+1.5=8(cm).
∵C是线段AB的中点,
∴CB=$\frac{1}{2}$AB=4cm,
∴CD=CB−BD=4−1.5=2.5(cm).
(2)示意图如图所示:

∵AB=AD−BD=6.5−1.5=5cm,
∴CB=$\frac{1}{2}$AB=2.5cm,
∴CD=CB+BD=4cm.
12. (2025·辽宁沈阳铁西区期中)(1)如图,点 C 在线段 AB 上,点 M 在线段 AC 上,点 N 在线段 BC 上.
①已知 $AC= 13$,$CB= 8$,若点 M,N 分别是 AC,BC 的中点,求线段 MN 的长;
②已知 $AC= 13$,$CB= 8$,若点 M 是 AC 的中点,$BN= \frac{3}{4}BC$,求线段 MN 的长;
③已知 $AC= a$,$CB= b$,若 $AM= \frac{2}{3}AC$,$BN= \frac{1}{3}BC$,请直接写出线段 MN 的长(用含 a,b 的式子表示).
(2)若点 C 在直线 AB 上,(1)中其他条件不变,已知 $AC= a$,$CB= \frac{3}{5}a$,$5AM= 3CM$,$3BN= 2CN$,请直接写出线段 MN 的长.
]

答案:
(1)①
∵点M,N分别是AC,BC的中点,
∴CM=$\frac{1}{2}$AC=$\frac{1}{2}$×13=6.5,CN=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4,
∴MN=CM+CN=6.5+4=10.5;
②
∵点M是AC的中点,BN=$\frac{3}{4}$BC,
∴CM=$\frac{1}{2}$AC=$\frac{1}{2}$×13=6.5,CN=$\frac{1}{4}$BC=$\frac{1}{4}$×8=2,
∴MN=CM+CN=6.5+2=8.5;
③
∵AM=$\frac{2}{3}$AC,BN=$\frac{1}{3}$BC,
∴CM=$\frac{1}{3}$AC=$\frac{1}{3}$a,CN=$\frac{2}{3}$BC=$\frac{2}{3}$b,
∴MN=CM+CN=$\frac{1}{3}$a+$\frac{2}{3}$b.
(2)
∵5AM=3CM,3BN=2CN,
∴CM=$\frac{5}{8}$AC=$\frac{5}{8}$a,CN=$\frac{3}{5}$BC=$\frac{3}{5}$×$\frac{3}{5}$a=$\frac{9}{25}$a,
当点C在线段AB上时,
MN=CM+CN=($\frac{5}{8}$+$\frac{9}{25}$)a=$\frac{197}{200}$a.
当点B在线段AC上时,MN=AC−AM−CN=a−$\frac{3}{8}$a−$\frac{9}{25}$a=($\frac{5}{8}$−$\frac{9}{25}$)a=$\frac{53}{200}$a.
综上所述,MN的长为$\frac{197}{200}$a或$\frac{53}{200}$a.