四、操作题。
16 个钉子在木板上钉成 $ 4 × 4 $ 的方阵,以其中的 4 个钉子为顶点用橡皮筋围成正方形,小明围了如图所示的一个正方形,想一想,一共可以围成多少个不同的正方形?
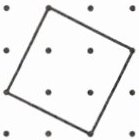
答案:20个 提示:

这样的有9个;

这样的有4个;

这样的有1个;

这样的有4个;小明所围那样的有2个,共20个。
1. $ A $ 和 $ B $ 都是自然数,且 $ A + B = 15 $,则 $ A $ 和 $ B $ 相乘的积最大是多少?
答案:7×8=56
解析:
当两个自然数的和一定时,这两个数越接近,它们的乘积越大。因为$A + B = 15$,所以当$A = 7$,$B = 8$时,两数最接近。此时$A × B = 7 × 8 = 56$。
56
2. 足球比赛,胜一场得 3 分,平一场得 1 分,输一场得 0 分,育才小学足球队已经比赛了 2 场,最多得多少分? 一共有多少种不同的得分情况?
答案:6分 6种
解析:
最多得分:$3 + 3 = 6$分
不同得分情况:
两场全胜:$3 + 3 = 6$分
一胜一平:$3 + 1 = 4$分
一胜一输:$3 + 0 = 3$分
两场平局:$1 + 1 = 2$分
一平一输:$1 + 0 = 1$分
两场全输:$0 + 0 = 0$分
共6种不同得分情况。
6分 6种
3. 小方有 1 元、5 元和 10 元的人民币各一张,妈妈有 5 元、10 元和 100 元的人民币各一张。每人各拿出一张,一共可以组成多少种不同的币值?
答案:8种
解析:
小方可能拿出:1元、5元、10元
妈妈可能拿出:5元、10元、100元
所有组合及币值:
1+5=6元
1+10=11元
1+100=101元
5+5=10元
5+10=15元
5+100=105元
10+5=15元
10+10=20元
10+100=110元
不同币值:6元、10元、11元、15元、20元、101元、105元、110元
共8种
4. 袁夏从少年宫出发经过邮局去图书馆,如果只向东走或向北走,一共有多少种不同的走法?

答案:6种
5. 有 9 厘米、7 厘米、5 厘米、4 厘米、12 厘米的小棒各一根,从中任意选三根,有多少种不同的选法? 如果把选出的三根小棒围成三角形,有多少种围法?
答案:10种 6种
解析:
从5根小棒中选3根的组合数:
$\binom{5}{3} = \frac{5!}{3!(5-3)!} = 10$
具体组合:(9,7,5)、(9,7,4)、(9,7,12)、(9,5,4)、(9,5,12)、(9,4,12)、(7,5,4)、(7,5,12)、(7,4,12)、(5,4,12)
能围成三角形的组合(满足两边之和大于第三边):
(9,7,5):$9+7>5$,$9+5>7$,$7+5>9$
(9,7,4):$9+7>4$,$9+4>7$,$7+4>9$
(9,7,12):$9+7>12$,$9+12>7$,$7+12>9$
(7,5,4):$7+5>4$,$7+4>5$,$5+4>7$
(9,5,12):$9+5>12$,$9+12>5$,$5+12>9$
(7,5,12):$7+5=12$,不满足
(9,4,12):$9+4=13>12$,$9+12>4$,$4+12>9$
(5,4,12):$5+4=9<12$,不满足
综上,不同选法10种,能围成三角形的6种。
10种 6种
6. 布袋中有 1 个红球、2 个黄球、3 个绿球,小明从袋中任意摸出 3 个球,可能会得到 3 个什么颜色的球? (列举出所有的可能)
答案:摸出一种颜色的球:3个绿球;摸出两种颜色的球:1个红球和2个黄球,1个红球和2个绿球,1个黄球和2个绿球,2个黄球和1个绿球;摸出三种颜色的球:1个红球、1个黄球和1个绿球。
7. 王叔叔家的新房装修结束,工人在他家的客厅里设置了三盏灯的位置。王叔叔到灯具店选购了红、黄、蓝、绿、紫五种颜色的灯各一盏。一共有多少种不同的安装灯的方法?
答案:10×6=60(种)
解析:
从五种颜色中选三盏灯的选法:$\text{C}_{5}^{3}=\frac{5!}{3!(5-3)!}=\frac{5×4×3!}{3!×2×1}=10$(种)
选出的三盏灯安装在三个位置的排法:$\text{A}_{3}^{3}=3!=3×2×1=6$(种)
总安装方法:$10×6=60$(种)
60
强基直通车 从 1 到 100 的自然数中,每次取两个数,要使它们的和大于 100,共有多少种取法?
答案:2500种 提示:根据题意,如果每次取出2个数的和大于100,那么两个数中至少有一个大于50,即可以分两种情况讨论:①若取出的2个数都大于50,就是从50个数中任意取2个数,则有50×49÷2=1225(种)取法。②若取出的2个数有一个小于或等于50,当取1时,另1个数只能取100,有1种取法;当取2时,另1个数只能取100或99,有2种取法……当取50时,另1个数只能取100,99,98,…,51中的一个,有50种取法,所以共有1+2+3+…+50=50×51÷2=1275(种)取法。综合①②可得,共有1225+1275=2500(种)取法。
解析:
①两个数都大于50时,从51到100这50个数中取2个数,取法有$\frac{50×49}{2}=1225$种。
②一个数小于或等于50,另一个数大于50时:
取1时,另一个数只能取100,有1种取法;
取2时,另一个数可取100、99,有2种取法;
……
取50时,另一个数可取51到100,有50种取法。
共有$1+2+\cdots+50=\frac{50×51}{2}=1275$种取法。
综合①②,总取法有$1225+1275=2500$种。
2500