9. 下面图形中共有几个长方形?
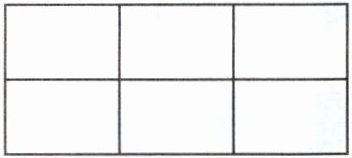
答案:18个
10. 林一和林乙是一对双胞胎,周末爸爸妈妈带着哥俩到假山下排成一排拍照,一共有多少种不同的站法?如果拍照时哥俩相邻站在一起,一共有多少种不同的站法?
答案:4×3×2×1=24(种) 3×2×1×2=12(种)
11. 李飞买一本笔记本,售价2元,如果他只有5角、2角和1角三种面值的人民币各若干张,那么一共有多少种不同的付费方法?
答案:29种
解析:
设5角、2角、1角的人民币分别用$x$张、$y$张、$z$张,$x,y,z$为非负整数。
总金额为2元=20角,可得方程:$5x + 2y + z = 20$,则$z = 20 - 5x - 2y$。
情况1:$x=0$
方程化为$2y + z = 20$,$y$可取$0,1,\cdots,10$,共11种。
情况2:$x=1$
方程化为$2y + z = 15$,$y$可取$0,1,\cdots,7$($2×7=14≤15$),共8种。
情况3:$x=2$
方程化为$2y + z = 10$,$y$可取$0,1,\cdots,5$,共6种。
情况4:$x=3$
方程化为$2y + z = 5$,$y$可取$0,1,2$($2×2=4≤5$),共3种。
情况5:$x=4$
方程化为$2y + z = 0$,$y=0,z=0$,共1种。
总计:$11+8+6+3+1=29$
29种
12. 有5把锁和5把钥匙,但不知道哪把钥匙开哪把锁,最多试开多少次,就一定能知道哪把钥匙开哪把锁?
答案:4+3+2+1+0=10(次)
13. A、B、C、D、E和F六个人进行围棋比赛,每两人之间赛1盘,现在A和B都赛了5盘,C赛了4盘,D和E都赛了3盘,则F赛了多少盘?
答案:F赛了2盘或4盘
解析:
A赛了5盘,与B、C、D、E、F各赛1盘;B赛了5盘,与A、C、D、E、F各赛1盘。此时C已赛2盘,D已赛2盘,E已赛2盘,F已赛2盘。
C需再赛2盘,分两种情况:
情况1:C与D、E赛,则D赛3盘(A、B、C),E赛3盘(A、B、C),F赛2盘(A、B)。
情况2:C与D、F赛,则D赛3盘(A、B、C),E需再赛1盘,只能与F赛,此时F赛4盘(A、B、C、E);同理C与E、F赛,F也赛4盘。
F赛了2盘或4盘。
14. 如图,一个圆上有8个点,经过任意三个点都可以画一个三角形,一共可以画多少个不同的三角形?

答案:56个 提示:假设这8个点分别是A、B、C、D、E、F、G、H。从A点出发,连接AB,然后以AB为三角形的一条边,分别与剩下6个点可连成6个三角形;连接AC,然后以AC为三角形的一条边,分别与剩下5个点可连成5个三角形(不再与B点连,否则会重复);连接AD……所以从A点出发,一共可以画6+5+4+3+2+1=21(个)不同的三角形。按照这样的方法,从B点出发,除去重复的一共可以画5+4+3+2+1=15(个)不同的三角形;从C点出发,除去重复的一共可以画4+3+2+1=10(个)不同的三角形;从D点出发,除去重复的一共可以画3+2+1=6(个)不同的三角形;从E点出发,除去重复的一共可以画2+1=3(个)不同的三角形;从F点出发,除去重复的只可以画1个三角形。因此,一共可以画21+15+10+6+3+1=56(个)不同的三角形。
解析:
从A点出发:$6+5+4+3+2+1=21$(个)
从B点出发:$5+4+3+2+1=15$(个)
从C点出发:$4+3+2+1=10$(个)
从D点出发:$3+2+1=6$(个)
从E点出发:$2+1=3$(个)
从F点出发:$1$(个)
一共:$21+15+10+6+3+1=56$(个)
56个
15. 某次数学测验一共出了5道题,评分方法如下:每答对一道题得5分,不答题得0分,答错一道题倒扣2分,每个考生预先给10分作为基础分。此次测验有多少种不同的分数?
答案:21种 提示:按照分别做对5、4、3、2、1、0道题的顺序,并考虑不答题的情况进行列举。做对5道题,最多得5×5+10=35(分);做对4道题,最多得5×4+0+10=30(分),还可能得30-2=28(分);做对3道题,最多得5×3+0+0+10=25(分),还可能得25-2=23(分),25-2-2=21(分);做对2道题,最多得5×2+0+0+0+10=20(分),还可能得20-2=18(分),20-2-2=16(分),20-2-2-2=14(分);做对1道题,最多得5×1+0+0+0+0+10=15(分),还可能得15-2=13(分),15-2-2=11(分),15-2-2-2=9(分),15-2-2-2-2=7(分);一道题都没答对,最多得0+10=10(分),还可能得10-2=8(分),10-2-2=6(分),10-2-2-2=4(分),10-2-2-2-2=2(分),10-2-2-2-2-2=0(分)。由以上可知,不同的分数共有1+2+3+4+5+6=21(种)。
解析:
做对5道题:得分$5×5 + 10 = 35$分,共1种分数;
做对4道题:最多$5×4 + 10 = 30$分,答错1道得$30 - 2 = 28$分,共2种分数;
做对3道题:最多$5×3 + 10 = 25$分,答错1道得$25 - 2 = 23$分,答错2道得$25 - 2×2 = 21$分,共3种分数;
做对2道题:最多$5×2 + 10 = 20$分,答错1道得$20 - 2 = 18$分,答错2道得$20 - 2×2 = 16$分,答错3道得$20 - 2×3 = 14$分,共4种分数;
做对1道题:最多$5×1 + 10 = 15$分,答错1道得$15 - 2 = 13$分,答错2道得$15 - 2×2 = 11$分,答错3道得$15 - 2×3 = 9$分,答错4道得$15 - 2×4 = 7$分,共5种分数;
做对0道题:最多$10$分,答错1道得$10 - 2 = 8$分,答错2道得$10 - 2×2 = 6$分,答错3道得$10 - 2×3 = 4$分,答错4道得$10 - 2×4 = 2$分,答错5道得$10 - 2×5 = 0$分,共6种分数;
不同分数总数:$1 + 2 + 3 + 4 + 5 + 6 = 21$种。
21
16. 一座99层摩天大楼的电梯上有显示楼层的液晶屏,如图,由于屏幕受到损坏,显示左边数字的7根线段中有1根不能亮了,显示右边数字的7根线段中有3根不能亮了。请问:电梯在运行的过程中,最多还有多少个楼层的数字显示是正确的?(9层及以下左边数字不显示)

答案:14个 提示:左边数字有1根线段坏了,最多有1、3、4、5、7和9,共6个数字显示正确;右边数字有3根线段坏了,最多有1、7或1、4,共2个数字显示正确。又9层及以下左边数字不显示。所以最多有14个楼层的数字显示是正确的,即1、11、31、41、51、71、91、4、14、34、44、54、74、94;或1、11、31、41、51、71、91、7、17、37、47、57、77、97。
解析:
左边数字1根线段损坏,可正确显示数字:1、3、4、5、7、9(共6个);右边数字3根线段损坏,可正确显示数字:1和7或1和4(共2个)。9层及以下左边不显示,仅右边正确数字有效。
情况1:右边正确数字为1、7
9层及以下:1、7(2个)
10-99层:左边6个数字分别与1、7组合,6×2=12个
共2+12=14个
情况2:右边正确数字为1、4
9层及以下:1、4(2个)
10-99层:左边6个数字分别与1、4组合,6×2=12个
共2+12=14个
最多14个楼层显示正确,具体楼层为1、11、31、41、51、71、91、4、14、34、44、54、74、94(或1、11、31、41、51、71、91、7、17、37、47、57、77、97)。
14