5. (1)如图①,每个小方格的边长是1厘米,求三角形ABC的面积。乐乐想,如果过点A作BC的平行线,把点A移动到某些格点上,使得面积不变,也能求出三角形的面积,方法更巧妙。请你帮乐乐标出移动后点A的位置,三角形ABC的面积是( )平方厘米。
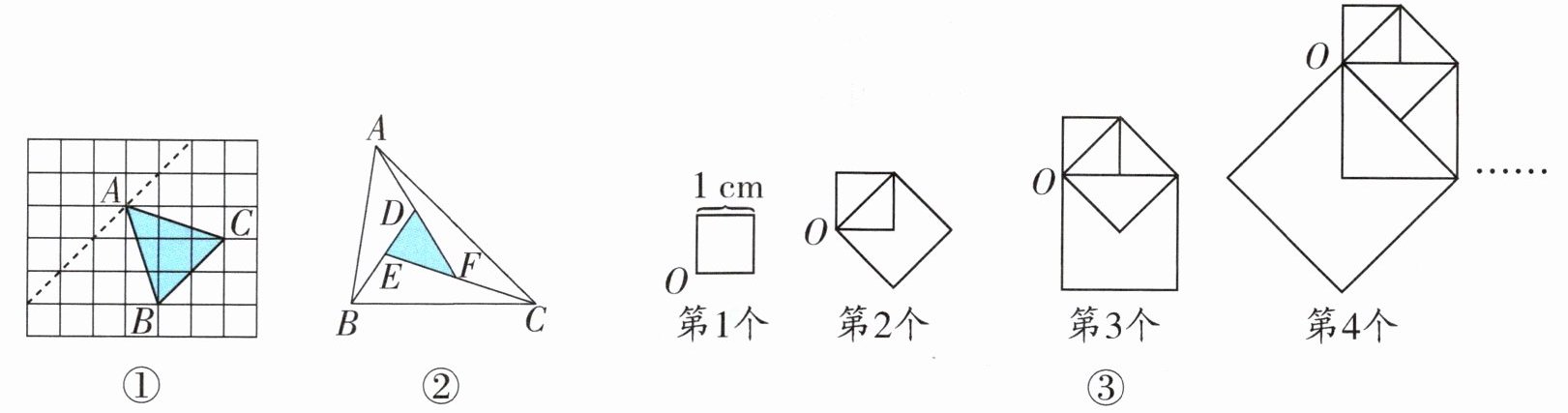
(2)如图②,把三角形DEF的各边向外延长1倍后得到三角形ABC,三角形ABC的面积为42平方厘米,三角形DEF的面积是( )平方厘米。
(3)如图③,从边长是1厘米的正方形的O点出发,以正方形的对角线为边长向同一侧连续画正方形,如图。第5个组合图形的面积是( )平方厘米。
答案:(1)
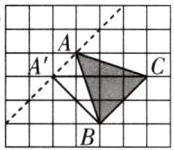
(标法不唯一) 4 提示:乐乐的做法是依据两条平行线之间的距离处处相等,即三角形的底 BC 不动,顶点 A 在平行于线段 BC 的直线上移动,这个顶点无论在哪儿,它到底 BC 的距离都不变,即高不变,因此三角形 ABC 的面积不变。如图,此时可以通过数格子得出$A'C = 4$厘米,$A'C$对应的高是 2 厘米,面积就是$4×2÷2 = 4$(平方厘米)。
(2)6 提示:先比较三角形 ABD 和三角形 DEF 的面积。这两个三角形的底边 AD 和 DF 相等,但是高不相等。如果把 AE 连接起来,如图所示,

三角形 ADE 与三角形 DEF 等底等高,所以它们的面积相等。注意到 E 是 BD 的中点,所以三角形 ABE 与三角形 ADE 的面积相等,因此三角形 ABD 的面积就是三角形 DEF 的面积的 2 倍。同理,三角形 BCE 和三角形 CAF 的面积都是三角形 DEF 面积的 2 倍,所以三角形 ABC 的面积就是三角形 DEF 面积的$2 + 2 + 2 + 1 = 7$倍,所以三角形 DEF 的面积就是$42÷7 = 6$(平方厘米)。
(3)23.5 提示:把原题图转化成下图:




由图可知,每个图形都是由若干个三角形组成的,其中三角形①的面积是$1×1÷2 = 0.5$(平方厘米),三角形②的面积是$0.5×2 = 1$(平方厘米),三角形③的面积是$1×2 = 2$(平方厘米),三角形④的面积是$2×2 = 4$(平方厘米)。发现:从三角形①开始,后一个三角形的面积都是前一个三角形面积的 2 倍,每个图形的最后两个三角形的面积相等。由此可总结出所得到的组合图形的面积规律,整理成表格如下。
图形序号 三角形个数 图形面积/$cm^{2}$
第 1 个 2 $0.5 + 0.5$
第 2 个 3 $0.5 + 1 + 1$
第 3 个 4 $0.5 + 1 + 2 + 2$
第 4 个 5 $0.5 + 1 + 2 + 4 + 4$
…… …… ……
由此可知,第 5 个组合图形中含有 6 个三角形,面积是$0.5 + 1 + 2 + 4 + 8 + 8 = 23.5$(平方厘米)。
6. 几何直观 如图,长方形ABCD的面积为100平方厘米。E、F、G分别为AB、BC、CD的中点,H为AD上任意的一点,求涂色部分的面积。

答案:$100÷2÷2 + 100÷2÷2 = 50$(平方厘米) 提示:连接 BH,三角形 BEH 和三角形 GDH 的底都是长方形宽的一半,高的和为长方形的长,因此这两个三角形的面积和为$100÷2÷2 = 25$(平方厘米)。三角形 BFH 的底是长方形长的一半,高为长方形的宽,因此它的面积为$100÷2÷2 = 25$(平方厘米),因此涂色部分的面积为$25 + 25 = 50$(平方厘米)。
解析:
连接 BH。
因为 E 是 AB 中点,G 是 CD 中点,设长方形长为 $ l $,宽为 $ w $,则 $ S_{ABCD}=lw=100 \, \text{cm}^2 $。
$ S_{\triangle BEH} + S_{\triangle GDH} = \frac{1}{2} × \frac{w}{2} × AH + \frac{1}{2} × \frac{w}{2} × HD = \frac{w}{4}(AH + HD) = \frac{w}{4}l = \frac{lw}{4} = \frac{100}{4} = 25 \, \text{cm}^2 $。
因为 F 是 BC 中点,$ S_{\triangle BFH} = \frac{1}{2} × \frac{l}{2} × w = \frac{lw}{4} = \frac{100}{4} = 25 \, \text{cm}^2 $。
涂色部分面积 = $ 25 + 25 = 50 \, \text{cm}^2 $。
答:涂色部分面积为 $ 50 \, \text{平方厘米} $。
7. 应用意识 如图,一台收割机在一块平行四边形田地上收割小麦,甲、乙两个直角三角形部分已经收割完毕,还有多少平方米的小麦需要收割?

答案:$80×60 + 40×120 = 9600$(平方米) $40×80÷2 = 1600$(平方米) $60×120÷2 = 3600$(平方米) $9600 - 1600 - 3600 = 4400$(平方米) 提示:一些不规则的、分散的几何图形可以经过分割、移补,拼成一个规则的几何图形,从而求出面积。如图,

将甲、乙两个三角形分别平移到①、②的位置,则平行四边形的面积是两个长方形面积之和,即$80×60 + 40×120 = 9600$(平方米),甲三角形的面积为$40×80÷2 = 1600$(平方米),乙三角形的面积为$60×120÷2 = 3600$(平方米),未收割部分的面积为$9600 - 1600 - 3600 = 4400$(平方米)。
8. 正方形ABCD的边长是8厘米,等腰直角三角形EFG的斜边FG长为26厘米。正方形与三角形放在同一条直线上,如图,CF= 10厘米。正方形以每秒2厘米的速度向右沿直线BC运动。

(1)当第6秒时,正方形ABCD与三角形EFG重叠部分的面积是( )平方厘米。
(2)第( )秒时,三角形与正方形重叠部分的面积是62平方厘米。
答案:(1)2
(2)12 或 15
提示:
(1)如图①所示:当第 6 秒时,

正方形向右运动:$2×6 = 12$(厘米),这时重叠面积为$2×2÷2 = 2$(平方厘米)。
(2)正方形的面积:$8×8 = 64$(平方厘米),$64 - 62 = 2$(平方厘米),即三角形与正方形的未重叠部分的面积是 2 平方厘米,分两种情况。
a.如图②所示:阴影三角形的面积为 2 平方厘米,此时正方形一共走的路程:$BB_{1}= 8 + 10 + 6 = 24$(厘米),$24÷2 = 12$(秒)。

b.如图③所示:阴影三角形的面积为 2 平方厘米,

此时正方形一共走的路程:$CC_{2}= 10 + 26 - 6 = 30$(厘米),$30÷2 = 15$(秒)。所以第 12 秒和 15 秒时,三角形与正方形的重叠部分面积是 62 平方厘米。
9. 如图所示,直角梯形ABCD的上底与高相等,正方形DEFH的边长是6厘米,涂色部分的面积是多少平方厘米?

答案:$6×6÷2 = 18$(平方厘米) 提示:观察题图,直角梯形 ADHB 的面积=$(AB + DH)×AD÷2$,直角三角形 ABE 的面积=$AB×(AD + DE)÷2$,因为$AB = AD$,四边形 DEFH 是正方形,所以直角梯形 ADHB 的面积=直角三角形 ABE 的面积。分别减去两个图形重叠的部分梯形 ABOD 的面积,得到三角形 BOH 的面积等于三角形 DOE 的面积,所以涂色部分的面积=三角形 DEH 的面积=正方形 DEFH 的面积÷2。
解析:
因为正方形$DEFH$的边长是$6$厘米,所以$DE = DH = 6$厘米,$\angle EDH = 90^\circ$。
由题意及图形关系可知,涂色部分的面积等于三角形$DEH$的面积。
三角形$DEH$的面积为:$\frac{1}{2} × DE × DH = \frac{1}{2} × 6 × 6 = 18$(平方厘米)。
答:涂色部分的面积是$18$平方厘米。