1. 项目化学习 根据表中的素材,探索完成任务。
|素材1|甲商场全场按标价打六折销售(六折即实际售价= 标价×0.6)|
|素材2|乙商场实行“满100元送100元购物券”的优惠,购物券可以在再次购买时冲抵现金(例如:某顾客购买衣服花费220元,赠券200元,再购买裤子时可冲抵现金,不再送券)|
|素材3|丙商场实行“满100元减50元”的优惠(例如:某顾客购物220元,他只需付款120元)|
问题解决:
任务1:三个商场同时出售一件标价为290元的上衣和一条标价为270元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场?
任务2:黄先生发现在甲、乙商场同时出售一件标价为380元的上衣和一条标价为300多元的裤子,在两家商场购买这一套衣服实际的付款额也一样,问:这条裤子的标价为多少元?
答案:任务1:290+270=560(元)
甲商场:560×0.6=336(元)
乙商场:290÷100=2(个)……90(元)
290+(270−100×2)=360(元)
丙商场:560÷100=5(个)……60(元) 560−50×5=310(元) 310<336<360 她应该选择丙商场
提示:根据三个商场的优惠方案,分别计算出实际付款的金额,选择最优惠的商场即可。
任务2:380×(1−0.6)=152(元) (300−152)÷(1−0.6)=370(元)
提示:380元的上衣在乙商场可得到300元的购物券,即在乙商场购买上衣和裤子共优惠了300元,所以在甲商场购买上衣和裤子也优惠了300元。
在甲商场购买上衣优惠了380×(1−0.6)=152(元),则购买裤子优惠了300−152=148(元),所以裤子的价格是148÷(1−0.6)=370(元)。
2. 规律探究问题 1899年,奥地利数学家皮克提出了著名的皮克公式:对于网格中顶点都在格点上的多边形,其面积= 内部的格点数+边界的格点数÷2 - 1。下面我们一起来探究吧。
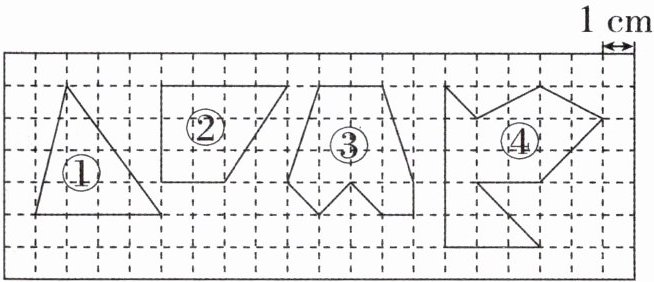
(1) 完成下面的表格。
|图形|①|②|③|④|
|内部的格点数(m)|6|
5
|
8
|
7
|
|边界的格点数(n)|6|
10
|
9
|
17
|
|m + n÷2 - 1|8|
9
|
11.5
|
14.5
|
|图形的面积$/cm^2$|8|
9
|
11.5
|
14.5
|
(2) 你能在图中画出一个边界有4个格点的,面积是1.5平方厘米的多边形吗?
不能,因为边界格点数为4,是2的倍数,而内部格点数一定是整数,所以这个多边形的面积一定是整数。
答案:(1)填表如下:
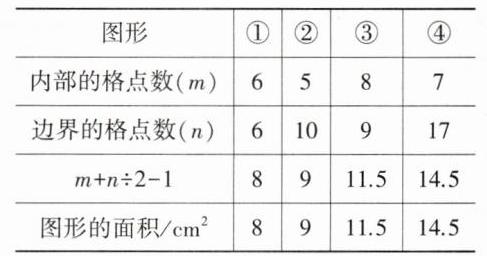
提示:在题图中数一数,填表并根据皮克公式计算即可。
(2)由于边界格点数为4,是2的倍数,而内部格点数一定是整数,所以这个多边形的面积一定是整数,因此,不能画出满足题意的多边形。