我们知道平行四边形的两组对边分别平行且相等,当四条边都相等时,就形成了一种特殊的平行四边形——菱形。除了四条边相等外,菱形还有哪些性质?请你量一量两条对角线形成的角度。(两个相对的角连成的线叫作对角线)
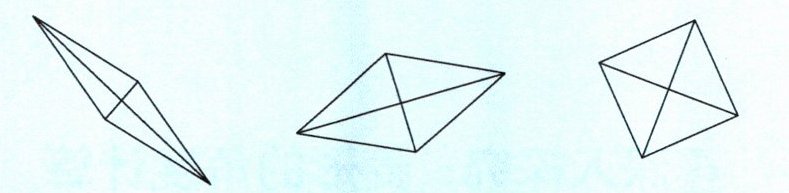
我发现:对角线互相( )。
答案:垂直
例1 如图,菱形的两条对角线分别为$AC = 10$厘米,$BD = 16$厘米,求菱形的面积。

我的思考

将菱形沿着线段$BD$分成两个三角形,这两个三角形完全相同。三角形$BAD$的面积= 线段$BD×$线段( )$÷ 2$,三角形$BCD$的面积= 线段$BD×$线段( )$÷ 2$。
菱形$ABCD$的面积= 三角形$BCD$的面积+三角形$ABD$的面积= 线段$BD×[$线段( )+线段( )$]÷ 2= 线段BD×$线段( )$÷ 2= $( )平方厘米。

将菱形补成一个长方形,这个长方形的长是( )厘米,宽是( )厘米。
对角线将长方形分成了四个相同的小长方形,将菱形分成了四个相同的小三角形,小三角形的面积是小长方形面积的( )。
长方形的面积= 线段$BD×线段AC$,菱形$ABCD$的面积= 线段( )$×$线段( )$÷ 2= $( )平方厘米。
我的结论
菱形的面积= 对角线的( )$÷ 2$
答案:解析:本题考查菱形面积的计算方法。对于菱形,其面积可以通过对角线来计算,公式为$S=\frac{1}{2}× d_1× d_2$(其中$S$表示菱形面积,$d_1$和$d_2$分别表示菱形的两条对角线长度)。已知菱形的两条对角线分别为$AC = 10$厘米,$BD = 16$厘米,将数值代入上述公式可得:$S=\frac{1}{2}×10×16$$=\frac{1}{2}×160$$ = 80$(平方厘米)答案:80平方厘米。AO CO CO AO AC 80 16 10 一半 BD AC 80 乘积
我的运用
如图,四边形$ABCD$是一个梯形,四边形$ABCE$是一个菱形,三角形$ABD$的面积是12平方厘米,那么菱形$ABCE$的面积是多少?线段$AC和线段BE$的乘积是多少?
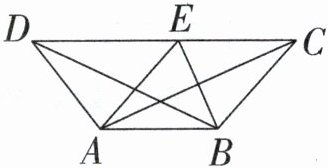
答案:三角形ABC的面积=三角形ABD的面积=
12平方厘米
菱形ABCE的面积=12x2=24(平方厘米)
线段ACx线段BE= 24x2=48