2025年学霸甘肃少年儿童出版社五年级数学上册苏教版第108页解析答案

例3 如图,梯形 $ABCD$ 中,$E$、$F$ 分别是腰 $AB$、$DC$ 的中点,$G$、$H$ 是所在线段上的任意一点。请分别验证下面两组图形中涂色部分的面积是梯形面积的一半。(第二组中,$EF$ 与 $AD$、$BC$ 平行)

我的思考

答案：一半一半

解析：

第一组图形中涂色部分的面积是梯形面积的一半；第二组图形中涂色部分的面积是梯形面积的一半。

1. 下面各梯形(图中除点 $A$、$B$、$C$、$D$ 以外,其余位于边上的点均为所在边的中点,梯形腰的中点连线与梯形的上、下底都平行)中,涂色部分的面积正好占整个梯形面积一半的有( )个。

A.1
B.2
C.3
D.4

答案：
D 提示:如图,根据等底同高的三角形面积相等,容易看出涂色部分的面积都占整个梯形面积的一半。

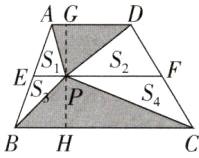
2. 如图,在梯形 $ABCD$ 中,$E$、$F$ 分别是腰 $AB$、$CD$ 的中点,$S_{1}$ 和 $S_{2}$ 的大小分别是 8 平方厘米和 18 平方厘米。梯形 $ABCD$ 的面积是多少平方厘米？

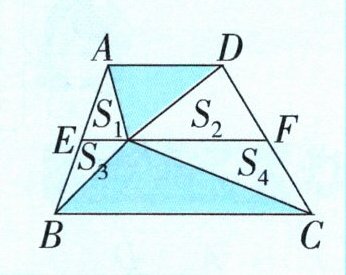
答案：
2×(2×18+2×8)=104(平方厘米) 提示:$S_{1}$和$S_{3}$等底同高,所以面积相等,$S_{2}$和$S_{4}$等底同高,所以面积相等。如图,GH过点P,G是AD上任意一点,H是BC上任意一点,根据例3可知,梯形CDGH的面积是三角形CDP面积的2倍,梯形ABHG的面积是三角形ABP面积的2倍,所以梯形ABCD的面积=2×(三角形CDP的面积+三角形ABP的面积)=2×(2×18+2×8)=104(平方厘米)。