1. 已知$\vert x\vert \lt a$,x是整数,若满足条件的值有7个,则a的值可能是 (
B
)
A.3
B.4
C.5
D.6
答案:B
解析:
解:由$|x| < a$得$-a < x < a$。
因为$x$是整数且满足条件的值有7个,所以这7个整数为$-3,-2,-1,0,1,2,3$。
则$3 < a \leq 4$,故$a$的值可能是4。
答案:B
2. 若$\vert a - 1\vert + \vert ab - 2\vert = 0$,则$\frac{1}{(a + 1)(b + 1)} + \frac{1}{(a + 2)(b + 2)} + … + \frac{1}{(a + 2024)(b + 2024)} = $
$\frac{506}{1013}$
。
答案:$\frac{506}{1013}$ 点拨:因为$|a-1|+|ab-2|=0$,所以$a-1=0,ab-2=0$,所以$a=1,b=2$,所以原式$=\frac{1}{2×3}+\frac{1}{3×4}+\cdots+\frac{1}{2025×2026}=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\cdots+\frac{1}{2025}-\frac{1}{2026}=\frac{1}{2}-\frac{1}{2026}=\frac{506}{1013}$.
解析:
解:因为$|a - 1| + |ab - 2| = 0$,且绝对值具有非负性,所以$a - 1 = 0$,$ab - 2 = 0$。
由$a - 1 = 0$,得$a = 1$。
将$a = 1$代入$ab - 2 = 0$,得$1×b - 2 = 0$,解得$b = 2$。
所以原式$=\frac{1}{(1 + 1)(2 + 1)} + \frac{1}{(1 + 2)(2 + 2)} + \cdots + \frac{1}{(1 + 2024)(2 + 2024)}$
$=\frac{1}{2×3} + \frac{1}{3×4} + \cdots + \frac{1}{2025×2026}$
因为$\frac{1}{n(n + 1)} = \frac{1}{n} - \frac{1}{n + 1}$,所以上式可裂项为:
$= (\frac{1}{2} - \frac{1}{3}) + (\frac{1}{3} - \frac{1}{4}) + \cdots + (\frac{1}{2025} - \frac{1}{2026})$
去括号后相互抵消,得:
$= \frac{1}{2} - \frac{1}{2026}$
$= \frac{1013}{2026} - \frac{1}{2026}$
$= \frac{1012}{2026}$
$= \frac{506}{1013}$
故答案为$\frac{506}{1013}$。
3. 数学实验室:
如图,点A,B在数轴上分别表示有理数a,b,A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离$AB= \vert a - b\vert$。
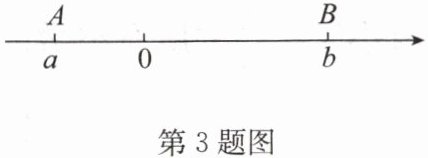
利用数形结合思想解答下列问题:
(1)数轴上表示2和6的两点之间的距离是
4
;数轴上表示1和-4的两点之间的距离是
5
;
(2)数轴上表示x和6的两点之间的距离为
|x-6|
;数轴上表示x和-3的两点之间的距离为
|x+3|
;
(3)若x表示一个有理数,则$\vert x - 1\vert + \vert x + 4\vert$的最小值为
5
;
(4)若x表示一个有理数,且$\vert x + 1\vert + \vert x - 3\vert = 4$,则满足条件的所有整数x的和为
5
;
(5)若x表示一个有理数,当$x=$
3
,式子$\vert x + 2\vert + \vert x - 3\vert + \vert x - 4\vert$有最小值为
6
。
答案:(1)4 5 (2)$|x-6|$ $|x+3|$ (3)5
(4)5 点拨:满足条件的x在-1和3之间,它们分别是-1,0,1,2,3,其和为5.
(5)3 6 点拨:因为式子$|x+2|+|x-3|+|x-4|$可看作是数轴上表示x的点到表示-2,3,4三点的距离之和,所以当$x=3$时,$|x+2|+|x-3|+|x-4|$有最小值,为$|3+2|+|3-3|+|3-4|=6$.