1. 在平面内,由不在同一条直线上的
三条或三条以上
的线段
首尾顺次
相接组成的图形叫作多边形. 这些线段叫作多边形的
边
,线段的公共端点叫作多边形的
顶点
.
2. 多边形
相邻
两边组成的角叫作多边形的内角,多边形的边与它
邻边的延长线
组成的角叫作多边形的外角.
3. 连接多边形
不相邻的两个顶点
的线段叫作多边形的对角线.
4. 各边
相等
、各内角也
相等
的多边形叫作正多边形.
答案:1.三条或三条以上 首尾顺次 边 顶点
2.相邻 邻边的延长线
3.不相邻的两个顶点
4.相等 相等
1. 从某多边形一个顶点出发连接其余各顶点得 7 条对角线,则这个多边形的边数为(
D
)
A.7
B.8
C.9
D.10
答案:D
解析:
解:设这个多边形的边数为$n$。
从$n$边形一个顶点出发可引$(n - 3)$条对角线。
已知对角线数量为$7$,则$n - 3=7$,解得$n = 10$。
答案:D
2. 已知正八边形的周长是 32 cm,则这个多边形的边长是
4
cm.
答案:4
解析:
正八边形有8条边,且各边相等。
边长 = 周长 ÷ 边数 = 32 ÷ 8 = 4 cm。
4
3. 若一个多边形的一个外角的度数是 40°,则与它相邻的内角度数是
140°
.
答案:140°
解析:
解:因为多边形的一个外角与它相邻的内角互补,即两角之和为180°,已知外角为40°,所以相邻内角度数为180° - 40° = 140°。
140°
4. a 个六边形、b 个五边形共有
6a+5b
条边.
答案:(6a+5b)
解析:
一个六边形有6条边,a个六边形共有6a条边;一个五边形有5条边,b个五边形共有5b条边。所以a个六边形、b个五边形共有边:6a + 5b 条。
(6a + 5b)
5. 一个多边形的边数的 2 倍与过一顶点的对角线条数的和等于 18,求这个多边形的边数.
答案:解:设多边形的边数为n,根据题意,得
2n+(n−3)=18,解得n=7.
答:这个多边形的边数为7.
6. 如图,∠B = 25°,∠BCD = 45°,∠CDE = 30°,∠E = 10°.
试说明:AB // EF.
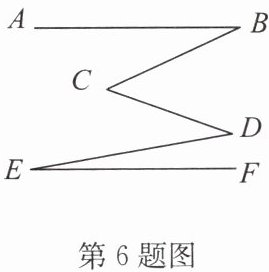
答案:解:如答图,过点C作CG//AB,过点D作DH//AB,
则CG//DH.
因为∠B=25°,所以∠BCG=25°.
因为∠BCD=45°,所以∠GCD=20°.
因为CG//HD,所以∠CDH=20°.
因为∠CDE=30°,所以∠HDE=10°,
所以∠HDE=∠E,所以DH//EF;
因为DH//AB,所以AB//EF;