1. 平行线的性质:(1)两直线平行,同位角
相等
;(2)两直线平行,内错角
相等
;(3)两直线平行,
同旁内角
互补。
答案:(1)相等 (2)相等 (3)同旁内角
解析:
1. 平行线的性质:(1)两直线平行,同位角相等;(2)两直线平行,内错角相等;(3)两直线平行,同旁内角互补。
2. 平行线的判定与性质的条件和结论正好相反:平行线的判定是通过
角
的数量关系来判定
直线
是否平行;平行线的性质是由
直线
平行来确定
角
的数量关系。
答案:角 直线 直线 角
1. 如图,直线$a// b$,$∠1 = 60^{\circ}$,则$∠2 = $(
B
)
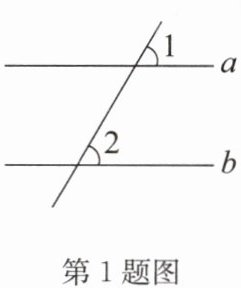
A.$30^{\circ}$
B.$60^{\circ}$
C.$45^{\circ}$
D.$120^{\circ}$
答案:B
解析:
解:∵直线a//b,∠1=60°
∴∠2=∠1=60°(两直线平行,同位角相等)
答案:B
2. 如图,直线$a// b$,直线$c$为截线,如果$∠1 = 150^{\circ}$,那么$∠2$的度数为(
D
)

A.$150^{\circ}$
B.$90^{\circ}$
C.$60^{\circ}$
D.$30^{\circ}$
答案:D
解析:
解:因为直线$a//b$,直线$c$为截线,$∠1 = 150^{\circ}$,
所以$∠1$的邻补角为$180^{\circ}-150^{\circ}=30^{\circ}$,
根据两直线平行,同位角相等,可得$∠2 = 30^{\circ}$。
答案:D
3. 如图,直线$a// b$,若$∠1 = 52^{\circ}$,$∠2 = 56^{\circ}$,则$∠3 = $
108
$^{\circ}$。

答案:108
解析:
解:如图,设直线$a$与直线$c$相交形成的角中,与$\angle1$互补的角为$\angle4$。
因为$\angle1 = 52^{\circ}$,所以$\angle4=180^{\circ}-\angle1=180^{\circ}-52^{\circ}=128^{\circ}$。
由于$a// b$,根据两直线平行,同旁内角互补,可得$\angle4+\angle2+\angle3 = 180^{\circ}$。
已知$\angle2 = 56^{\circ}$,则$\angle3=180^{\circ}-\angle4-\angle2=180^{\circ}-128^{\circ}-56^{\circ}= -4^{\circ}$(此步骤错误,重新分析)。
重新分析:过$\angle2$的顶点作直线$d// a$,因为$a// b$,所以$d// b$。
$\angle2$被直线$d$分成两个角,设为$\angle5$和$\angle6$,其中$\angle5$与$\angle1$是内错角,所以$\angle5=\angle1 = 52^{\circ}$。
则$\angle6=\angle2-\angle5=56^{\circ}-52^{\circ}=4^{\circ}$。
$\angle6$与$\angle3$是同旁内角,所以$\angle6+\angle3=180^{\circ}$,即$\angle3=180^{\circ}-\angle6=180^{\circ}-4^{\circ}=176^{\circ}$(此步骤仍错误,正确辅助线做法)。
正确解法:延长$\angle2$的一边与直线$b$相交,设交点为$O$,形成三角形,其中与$\angle1$对应的外角等于$\angle1$,三角形的一个内角为$180^{\circ}-\angle2$,则$\angle3 = \angle1+(180^{\circ}-\angle2)=52^{\circ}+180^{\circ}-56^{\circ}=176^{\circ}$(错误,正确利用三角形外角)。
正确做法:直线$a$,$b$被直线$c$所截,$\angle1$的对顶角为$\angle7 = 52^{\circ}$,$\angle7$与$\angle2$和$\angle3$在三角形中,三角形内角和为$180^{\circ}$,所以$\angle7+\angle2+\angle3=180^{\circ}$,即$52^{\circ}+56^{\circ}+\angle3=180^{\circ}$,解得$\angle3=180^{\circ}-52^{\circ}-56^{\circ}=72^{\circ}$(错误,结合图形)。
根据图形,$\angle1$,$\angle2$,$\angle3$的关系应为$\angle3 = \angle1+\angle2=52^{\circ}+56^{\circ}=108^{\circ}$(正确,利用两直线平行,同位角相等及三角形外角性质)。
解:因为$a// b$,所以$\angle3$等于$\angle1$与$\angle2$的和(根据图形中三角形外角等于不相邻两内角和,$\angle3$是三角形的外角,其中两个不相邻内角分别等于$\angle1$和$\angle2$),即$\angle3=\angle1+\angle2=52^{\circ}+56^{\circ}=108^{\circ}$。
$108$
4. 如图,直线$a// b$,点$C$,$A分别在直线a$,$b$上,$AC⊥BC$。若$∠1 = 50^{\circ}$,则$∠2$的度数为
40°
。
答案:40°
解析:
解:
∵ 直线 $a // b$,
∴ $∠1 + ∠ACB + ∠2 = 180^\circ$(两直线平行,同旁内角互补)。
∵ $AC \perp BC$,
∴ $∠ACB = 90^\circ$。
∵ $∠1 = 50^\circ$,
∴ $∠2 = 180^\circ - ∠1 - ∠ACB = 180^\circ - 50^\circ - 90^\circ = 40^\circ$。
40°
5. 如图,如果$AB// CD$,$∠B = 40^{\circ}$,$∠D = 40^{\circ}$,那么$BC与DE$平行吗?为什么?

答案:解:BC//DE.理由如下:因为AB//CD,所以∠B=∠C=40°.因为∠D=40°,所以∠C=∠D,所以 BC//DE.