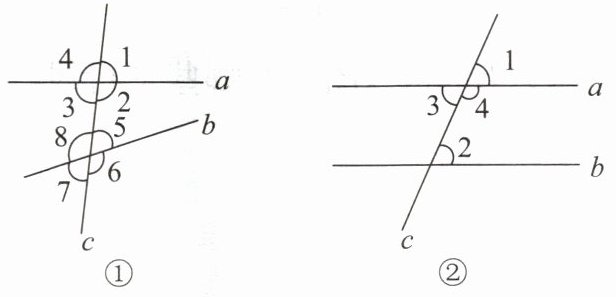
1. 如图①,直线a,b被直线c所截,所形成的八个角中,$∠3和∠5$这样的两个角叫作
内错
角,$∠2和∠5$这样的两个角叫作
同旁内
角,图①中的内错角共有
2
对,同旁内角共有
2
对。
答案:内错 同旁内 2 2
2. 两条直线被第三条直线所截,如果内错角
相等
,那么这两条直线平行。(简单说成:
内错角相等,两直线平行
。)如图②,若
∠2=∠3
,则$a// b$。
答案:相等 内错角相等,两直线平行 ∠2=∠3
3. 两条直线被第三条直线所截,如果同旁内角
互补
,那么这两条直线平行。(简单说成:
同旁内角互补,两直线平行
。)如图②,若
∠2+∠4=180°
,则$a// b$。
答案:互补 同旁内角互补,两直线平行 ∠2+∠4=180°
1. 如图,下列条件能说明$AB// CD$的是 (
C
)

A.$∠A+∠B= 180^{\circ }$
B.$∠A= ∠C$
C.$∠A+∠C= 180^{\circ }$
D.$∠B= ∠D$
答案:C
解析:
要说明$AB// CD$,需依据平行线的判定定理分析各选项:
选项A:$\angle A + \angle B = 180^\circ$,$\angle A$与$\angle B$是同旁内角,它们互补只能说明$AD// BC$,无法判定$AB// CD$。
选项B:$\angle A = \angle C$,$\angle A$与$\angle C$是四边形的对角,不是同位角、内错角或同旁内角,不能作为判定$AB// CD$的依据。
选项C:$\angle A + \angle C = 180^\circ$,$\angle A$与$\angle C$是同旁内角,根据“同旁内角互补,两直线平行”,可判定$AB// CD$。
选项D:$\angle B = \angle D$,$\angle B$与$\angle D$是四边形的对角,不是同位角、内错角或同旁内角,不能判定$AB// CD$。
答案:C
2. 如图,下列条件中,不能判定直线$l_{1}// l_{2}$的是 (
C
)
A.$∠1= ∠3$
B.$∠4= ∠5$
C.$∠1= ∠2$
D.$∠2+∠4= 180^{\circ }$
答案:C
解析:
解:A. ∠1=∠3,内错角相等,两直线平行,能判定l₁//l₂;
B. ∠4=∠5,同位角相等,两直线平行,能判定l₁//l₂;
C. ∠1=∠2,无法判定l₁//l₂;
D. ∠2+∠4=180°,同旁内角互补,两直线平行,能判定l₁//l₂。
答案:C