1. 如果两条直线相交所成的四个角中有一个角是
直角
,那么就称这两条直线互相垂直,其中的一条直线叫作另一条直线的
垂线
,它们的交点叫作
垂足
.
2. 与垂直有关的推理:(1)因为$\angle 1= 90^{\circ}$,所以$a\perp b$;(2)因为$a\perp b$,所以$\angle 1= 90^{\circ}$.
3. 基本事实:在同一平面内,过一点有且只有
一
条直线与已知直线垂直.
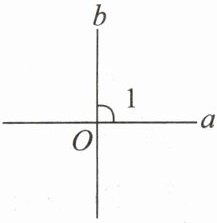
答案:1.直角 垂线 垂足 3.一
1. 如图,点$O在直线DB$上,$OA\perp OC$,$\angle 1= 20^{\circ}$,则$\angle 2$的度数为(
C
)
A.$150^{\circ}$
B.$120^{\circ}$
C.$110^{\circ}$
D.$100^{\circ}$
答案:C
2. 如图,$AO\perp BC$,$OM\perp ON$,则图中互余的角有(
B
)
A.$3$对
B.$4$对
C.$5$对
D.$6$对
答案:B
解析:
解:∵AO⊥BC,OM⊥ON,
∴∠AOB=∠AOC=∠MON=90°,
∴∠AOM+∠BOM=90°,∠AON+∠CON=90°,∠AOM+∠AON=90°,∠BOM+∠CON=90°,
∴互余的角有4对。
答案:B
3. 如图,$O为直线AB$上一点,$OC\perp OD$,如果$\angle 1= 35^{\circ}$,那么$\angle 2$的度数是
55°
.
答案:55°
解析:
解:因为O为直线AB上一点,所以∠AOB=180°。
因为OC⊥OD,所以∠COD=90°。
又因为∠1+∠COD+∠2=∠AOB,∠1=35°,
所以∠2=∠AOB - ∠1 - ∠COD=180° - 35° - 90°=55°。
55°
4. 如图,$O为直线AB$上一点,$\angle BOC= 36^{\circ}$,$OD平分\angle AOC$,$OD\perp OE$. 求$\angle AOE$的度数.

答案:解:因为∠AOC+∠BOC=180°,所以∠AOC=180°-∠BOC=180°-36°=144°.因为 OD 平分∠AOC,所以∠AOD=1/2∠AOC=72°.因为OD⊥OE,所以∠DOE=90°,所以∠AOE=∠DOE-∠AOD=90°-72°=18°.