1. 有
公共端点
的两条射线组成的图形叫作角,这个公共端点是角的
顶点
,这两条射线是角的
两条边
. 角也可以看成是一条
射线
绕着它的
端点
旋转到另一个位置所形成的图形.
2. 角的表示方法:(1)用三个大写字母表示,表示顶点的字母必须写在
中间
;(2)当以某个点为顶点的角只有 1 个时,角可以用它的
顶点
字母来表示;(3)在角的内部靠近顶点处画上弧线,注上 1 个数字或希腊字母后,角可以用 1 个
数字
或
希腊字母
来表示.
3. 角的常用度量单位是
度
、
分
、
秒
. 相邻单位之间的进率是
60
.
答案:1. 公共端点 顶点 两条边 射线 端点
2. (1)中间 (2)顶点 (3)数字 希腊字母
3. 度 分 秒 60
1. 如图,能用一个大写字母表示的角有 (
B
)
A.1 个
B.2 个
C.3 个
D.4 个
答案:B
解析:
解:观察图形可知,顶点处只有一个角的顶点为A和B。
顶点A处只有∠A,顶点B处只有∠B。
顶点C处有∠ACB和∠BCD两个角,不能用一个大写字母表示。
能用一个大写字母表示的角有2个。
答案:B
2. 下列各角中,不可能是钝角的是 (
D
)
A.$\frac{1}{3}$周角
B.$\frac{2}{3}$平角
C.$\frac{2}{3}$钝角
D.$\frac{2}{3}$直角
答案:D
解析:
解:
A. 周角为$360^\circ$,$\frac{1}{3}$周角$=360^\circ×\frac{1}{3}=120^\circ$,是钝角;
B. 平角为$180^\circ$,$\frac{2}{3}$平角$=180^\circ×\frac{2}{3}=120^\circ$,是钝角;
C. 设钝角为$\alpha(90^\circ<\alpha<180^\circ)$,$\frac{2}{3}\alpha$的范围为$60^\circ<\frac{2}{3}\alpha<120^\circ$,可能为钝角;
D. 直角为$90^\circ$,$\frac{2}{3}$直角$=90^\circ×\frac{2}{3}=60^\circ$,不是钝角。
答案:D
3. (1)$48.12^{\circ}=$
48
$^{\circ}$
7
$'$
12
$''$;(2)$50^{\circ}7'30''= $
50.125
$^{\circ}$.
答案:(1)48 7 12 (2)50.125
解析:
(1) $0.12^{\circ} = 0.12 × 60' = 7.2'$,$0.2' = 0.2 × 60'' = 12''$,所以$48.12^{\circ} = 48^{\circ}7'12''$
(2) $30'' = 30 ÷ 60' = 0.5'$,$7.5' = 7.5 ÷ 60^{\circ} = 0.125^{\circ}$,所以$50^{\circ}7'30'' = 50.125^{\circ}$
(1)48 7 12;(2)50.125
4. 计算:
(1)$53^{\circ}28'+47^{\circ}32'$;
(2)$17^{\circ}50'-3^{\circ}27'$.
答案:(1)$101^{\circ }$ (2)$14^{\circ }23'$
解析:
(1) $53^{\circ}28' + 47^{\circ}32'$
$=(53^{\circ} + 47^{\circ}) + (28' + 32')$
$=100^{\circ} + 60'$
$=100^{\circ} + 1^{\circ}$
$=101^{\circ}$
(2) $17^{\circ}50' - 3^{\circ}27'$
$=(17^{\circ} - 3^{\circ}) + (50' - 27')$
$=14^{\circ} + 23'$
$=14^{\circ}23'$
5. 如图,解答下列问题.
(1)写出图中能用一个字母表示的角;
(2)写出以 B 为顶点的角;
(3)图中共有几个角(不含平角)? 分别把它们表示出来.
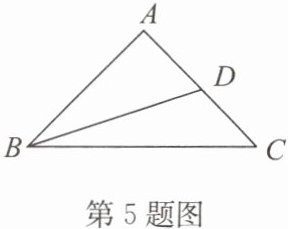
答案:解:(1)能用一个字母表示的角有$∠A,∠C.$
(2)以 B 为顶点的角有$∠ABD,∠DBC,∠ABC.$
(3)共有 7 个角,分别是$∠A,∠ABD,∠DBC,∠ABC,∠C,∠ADB,∠BDC.$