25. (10分)如图,$∠1= ∠2,CF⊥AB,DE⊥AB$,试确定FG与BC的位置关系,并说明理由.
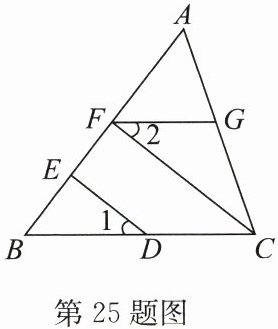

答案:解:FG//BC,理由如下:因为CF⊥AB,DE⊥AB,所以∠BED=90°,∠BFC=90°,所以∠BED=∠BFC,所以ED//FC,所以∠1=∠BCF.因为∠1=∠2,所以∠2=∠BCF,所以FG//BC.
26. (10分)规定一种新运算法则:$a※b= a^{2}+2ab$,例如,$3※(-2)= 3^{2}+2×3×(-2)= -3$.
(1)求$(-2)※3$的值;
(2)若$1※x= 3$,求$(-2)※x$的值.
答案:(1)求(-2)※3的值;解:原式=(-2)²+2×(-2)×3=4-12=-8.(2)若1※x=3,求(-2)※x的值;解:因为1※x=3,所以1²+2×1×x=3,解得x=1,所以(-2)※x=(-2)※1=(-2)²+2×(-2)×1=4-4=0.
27. (12分)自来水公司为限制开发区单位用水,规定某单位每月计划内用水300吨,计划内用水每吨收费3元,超计划部分每吨按4元收费.
(1)某月该单位用水260吨,水费是
780
元;若用水350吨,则水费是
1100
元;
(2)设该单位每月用水量为x吨,填表:(用含x的代数式表示)
3x
4x-300
(3)若某月该单位缴纳水费1300元,则该单位这个月用水多少吨?
解:设单位这个月用水x吨,易知x>300.由题意,得4x-300=1300,解得x=400.答:该单位这个月用水400吨.
答案:(1)780 1100 (2)3x 4x-300 (3)解:设单位这个月用水x吨,易知x>300.由题意,得4x-300=1300,解得x=400.答:该单位这个月用水400吨.
28. (12分)如图,在数轴上点A表示的数是-4,点B在点A的右侧,且到点A的距离是24,点C在点A与点B之间,且$BC= 3AC$.
(1)点B表示的数是
20
,点C表示的数是
2
.
(2)若点P从点A出发,沿数轴以每秒3个单位长度的速度向右匀速运动,同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒,在运动过程中,
①当t为何值时,点P与点Q相遇?
②当t为何值时,点P与点Q间的距离为9个单位长度?
(3)在(2)的条件下,在运动过程中,是否存在某一时刻使得$PC+QB= 7$? 若存在,请求出此时点P表示的数;若不存在,请说明理由.
(2)①解:由题意,得$3t + 2t=24$,解得$t = 4.8$。
②解:由题意,得$3t + 2t + 9=24$或$3t + 2t - 9=24$,解得$t = 3$或$t = 6.6$。
(3)解:存在。当点$P$在线段$AC$上时,$6 - 3t + 2t=7$,解得$t=-1$(不合题意,舍去);当点$P$在线段$BC$上时,$3t - 6 + 2t=7$,解得$t = 2.6$,此时点$P$表示的数为$-4+3×2.6 = 3.8$。综上,点$P$表示的数为$3.8$。
答案:(1)20;2
(2)①解:由题意,得$3t + 2t=24$,解得$t = 4.8$。
②解:由题意,得$3t + 2t + 9=24$或$3t + 2t - 9=24$,解得$t = 3$或$t = 6.6$。
(3)解:存在。当点$P$在线段$AC$上时,$6 - 3t + 2t=7$,解得$t=-1$(不合题意,舍去);当点$P$在线段$BC$上时,$3t - 6 + 2t=7$,解得$t = 2.6$,此时点$P$表示的数为$-4+3×2.6 = 3.8$。综上,点$P$表示的数为$3.8$。