20.(8分)已知一个角的补角比这个角的余角的3倍大$ 20^{\circ} $,求这个角的度数.
答案:解:设这个角的度数是x°,则其余角是(90 - x)°,补角是(180 - x)°.根据题意,得(180 - x) - 3(90 - x)=20,解得x = 55.答:这个角的度数为55°.
解析:
解:设这个角的度数是$x^{\circ}$,则其余角是$(90 - x)^{\circ}$,补角是$(180 - x)^{\circ}$。根据题意,得$(180 - x) - 3(90 - x)=20$,解得$x = 55$。答:这个角的度数为$55^{\circ}$。
21.(8分)(2024·泗洪期中)如图,$ AB// CD $,$ \angle CED= 90^{\circ} $,$ \angle BED= 30^{\circ} $,求$ \angle C $的度数.
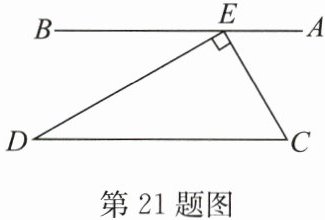
答案:解:因为∠CED = 90°,∠BED = 30°(已知),所以∠AEC = 180° - ∠BED - ∠CED = 60°(平角定义).因为AB//CD(已知),所以∠C = ∠AEC = 60°(两直线平行,内错角相等).
22.(8分)如图,直线$ AB 与 CD 相交于点 O $,$ OF\perp OC $,$ \angle BOC:\angle BOE= 1:3 $,$ \angle AOF= 2\angle COE $.求$ \angle COE $的度数.

答案:解:设$\angle BOC = x$.
因为$\angle BOC:\angle BOE = 1:3$,所以$\angle BOE = 3x$,则$\angle COE=\angle BOE - \angle BOC=3x - x=2x$.
因为$\angle AOF = 2\angle COE$,所以$\angle AOF = 2×2x = 4x$.
因为$OF\perp OC$,所以$\angle FOC = 90^\circ$.
又因为$\angle AOD=\angle BOC = x$(对顶角相等),且$\angle AOD+\angle AOF+\angle FOC = 180^\circ$(平角定义),
所以$x + 4x+90^\circ=180^\circ$,即$5x=90^\circ$,解得$x = 18^\circ$.
所以$\angle COE=2x = 2×18^\circ=36^\circ$.
23.(10分)已知线段$ AB= 10 \mathrm{cm} $,直线$ AB 上有一点 C $,且$ BC= 4 \mathrm{cm} $,$ M 是 AC $的中点,求线段$ AM $的长.
答案:解:如答图①,当点C在线段AB的延长线上时,因为AB = 10 cm,BC = 4 cm,所以AC = AB + BC = 10 + 4 = 14(cm).因为M是AC的中点,所以AM = $\frac{1}{2}$AC = $\frac{1}{2}$×14 = 7(cm).如答图②,当点C在线段AB上时,因为AB = 10 cm,BC = 4 cm,所以AC = AB - BC = 10 - 4 = 6(cm).因为M是AC的中点,所以AM = $\frac{1}{2}$AC = $\frac{1}{2}$×6 = 3(cm).综上所述,线段AM的长为7 cm或3 cm.

解析:
当点C在线段AB的延长线上时,
因为$AB = 10\ \text{cm}$,$BC = 4\ \text{cm}$,
所以$AC = AB + BC = 10 + 4 = 14\ \text{cm}$。
因为M是AC的中点,
所以$AM=\frac{1}{2}AC=\frac{1}{2}×14 = 7\ \text{cm}$。
当点C在线段AB上时,
因为$AB = 10\ \text{cm}$,$BC = 4\ \text{cm}$,
所以$AC=AB - BC=10 - 4 = 6\ \text{cm}$。
因为M是AC的中点,
所以$AM=\frac{1}{2}AC=\frac{1}{2}×6 = 3\ \text{cm}$。
综上所述,线段AM的长为$7\ \text{cm}$或$3\ \text{cm}$。
解:因为$ DF 平分 \angle ADE $,$ \angle ADE= 60^{\circ} $(已知),
所以
∠EDF
$ =\frac{1}{2}\angle ADE= 30^{\circ} $(
角平分线定义
).
因为$ \angle 1= 30^{\circ} $(已知),
所以
∠1
=
∠EDF
(
等量代换
).
所以$ DF// BE $(
内错角相等,两直线平行
).
答案:∠EDF 角平分线定义 ∠1 ∠EDF 等量代换 内错角相等,两直线平行
解析:
因为$DF$平分$\angle ADE$,$\angle ADE = 60^{\circ}$(已知),
所以$\angle EDF=\frac{1}{2}\angle ADE = 30^{\circ}$(角平分线定义)。
因为$\angle 1 = 30^{\circ}$(已知),
所以$\angle 1=\angle EDF$(等量代换)。
所以$DF// BE$(内错角相等,两直线平行)。
25.(10分)(2024·宿城期末)如图,直线$ AB 与 CD 相交于点 O $,$ OE\perp AB $,$ OF\perp CD $.
(1)图中与$ \angle COE $互补的角是______
∠EOD,∠AOF
;(把符合条件的角都写出来)
(2)若$ \angle AOD= \frac{1}{5}\angle EOF $,求$ \angle AOD $的度数.

解:设∠AOD = x,则∠EOF = 5x,因为∠AOD = ∠BOC(对顶角相等),所以∠BOC = x.因为OE⊥AB,OF⊥CD,所以∠BOE = 90°,∠COF = 90°,所以∠EOC = ∠BOE - ∠BOC = 90° - x,所以∠EOF = ∠EOC + ∠COF = 90° - x + 90° = 5x,即6x = 180°,解得x = 30°,所以∠AOD = 30°.
答案:(1)∠EOD,∠AOF
(2)解:设∠AOD = x,则∠EOF = 5x,因为∠AOD = ∠BOC(对顶角相等),所以∠BOC = x.因为OE⊥AB,OF⊥CD,所以∠BOE = 90°,∠COF = 90°,所以∠EOC = ∠BOE - ∠BOC = 90° - x,所以∠EOF = ∠EOC + ∠COF = 90° - x + 90° = 5x,即6x = 180°,解得x = 30°,所以∠AOD = 30°.