18. (12分)(1)如图,在几何体下面的横线上写出它们的名称;
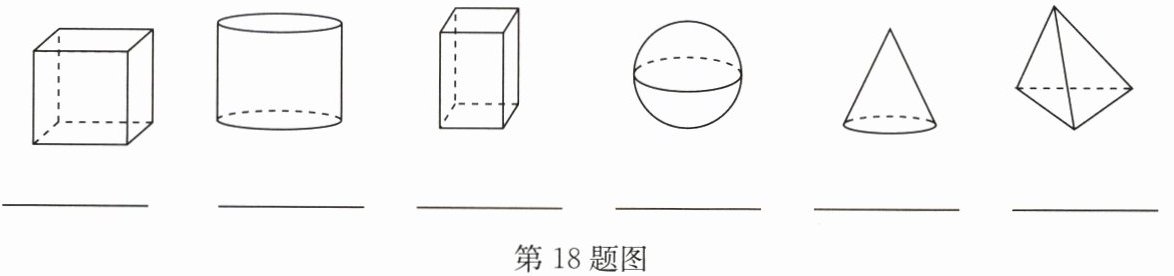
正方体 圆柱 长方体 球 圆锥 三棱锥
(2)将这些几何体分类,并写出分类依据.
解:①柱体有正方体、圆柱、长方体;锥体有圆锥、三棱锥;球体有球.
②有顶点的有正方体、长方体、圆锥、三棱锥;无顶点的有圆柱、球.
③有曲面的有圆柱、球、圆锥;无曲面的有正方体、长方体、三棱锥.
答案:(1)正方体 圆柱 长方体 球 圆锥 三棱锥
(2)解:①柱体有正方体、圆柱、长方体;锥体有圆锥、三棱锥;球体有球.
②有顶点的有正方体、长方体、圆锥、三棱锥;无顶点的有圆柱、球.
③有曲面的有圆柱、球、圆锥;无曲面的有正方体、长方体、三棱锥.
19. (12分)如图①,有一张长6cm,宽4cm的长方形纸板,现要求以其一组对边中点所在直线为轴旋转180°,可按两种方案进行操作.
方案一:以较长的一组对边中点所在直线为轴旋转,如图②.
方案二:以较短的一组对边中点所在直线为轴旋转,如图③.
(1)上述操作能形成的几何体是
圆柱
,说明的事实是
面动成体
;
(2)请通过计算说明哪种方案得到的几何体的体积大.

(2)解:方案一:π×$(\frac{6}{2})^{2}×4=36π(cm^{3})$,
方案二:π×$(\frac{4}{2})^{2}×6=24π(cm^{3})$,
36π>24π,所以方案一得到的几何体的体积大.
答案:(1)圆柱 面动成体
(2)解:方案一:π×$(\frac{6}{2})^{2}×4=36π(cm^{3})$,
方案二:π×$(\frac{4}{2})^{2}×6=24π(cm^{3})$,
36π>24π,所以方案一得到的几何体的体积大.
20. (12分)如图①所示的三棱柱,高为7cm,底面是一个边长为5cm的等边三角形.
(1)这个三棱柱有______条棱,有______个面;
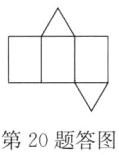
(2)图②方框中的图形是该三棱柱的表面展开图的一部分,请将它补全;
(3)要将该三棱柱沿某些棱剪开,展开成一个平面图形,需剪开______条棱,需剪开棱的棱长的和的最大值为______cm.

答案:(1)9 5
(2)解:如答图所示.(答案不唯一)
(3)5 31