7. (2024·姜堰期末)下列变形中,不正确的是(
B
)
A.若$x= y$,则$3x= 3y$
B.若$x= y$,则$x+2= y-1$
C.若$x= y$,则$x^{2}= y^{2}$
D.若$x= y$,则$1-x= 1-y$
答案:B
8. 如果$ma= mb$,那么下列等式不一定成立的是(
D
)
A.$ma+3= mb+3$
B.$ma-2= mb-2$
C.$-\frac {1}{3}ma= -\frac {1}{3}mb$
D.$a= b$
答案:D
解析:
当$ma = mb$时:
选项A:等式两边同时加3,得$ma + 3 = mb + 3$,成立;
选项B:等式两边同时减2,得$ma - 2 = mb - 2$,成立;
选项C:等式两边同时乘$-\frac{1}{3}$,得$-\frac{1}{3}ma = -\frac{1}{3}mb$,成立;
选项D:当$m = 0$时,无论$a$、$b$为何值,$ma = mb$都成立,但$a$不一定等于$b$,故不一定成立。
D
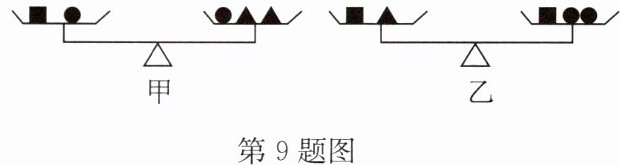
9. (2024·贵州)小红学习了等式的性质后,在甲、乙两台天平的左右两边分别放入“■”“●”“▲”三种物体,如图所示,天平都保持平衡. 若设“■”与“●”的质量分别为$x,y$,则下列关系式正确的是(
C
)
A.$x= y$
B.$x= 2y$
C.$x= 4y$
D.$x= 5y$
答案:C
解析:
设“▲”的质量为$z$。
由甲天平平衡得:$x + y = y + 2z$,化简得$x = 2z$。
由乙天平平衡得:$x + z = x + 2y$,化简得$z = 2y$。
将$z = 2y$代入$x = 2z$,得$x = 2×2y = 4y$。
C
10. 若$3x^{2}-4x-5= 7$,则$x^{2}-\frac {4}{3}x=$
4
.
答案:4
解析:
$3x^{2}-4x-5=7$
$3x^{2}-4x=12$
$x^{2}-\frac{4}{3}x=4$
4
11. 有下列说法:①由$a= b$,得$5-2a= 5-2b$;②由$a= b$,得$ac= bc$;③由$a= b$,得$\frac {a}{c}= \frac {b}{c}$;④由$\frac {a}{2c}= \frac {b}{3c}$,得$3a= 2b$;⑤由$a^{2}= b^{2}$,得$a= b$.其中正确的是
①②④
.(填序号)
答案:
①②④
12. 在下列各题的横线上填上适当的数或整式,使所得结果仍是等式,并说明是根据等式的哪一条性质以及是怎样变形的.
(1)如果$-\frac {x}{10}= \frac {y}{5}$,那么$x=$
-2y
,根据
等式的基本性质2,两边都乘-10
;
(2)如果$-2x= 2y$,那么$x=$
-y
,根据
等式的基本性质2,两边都除以-2
;
(3)如果$\frac {2}{3}x= 4$,那么$x=$
6
,根据
等式的基本性质2,两边都乘$\frac{3}{2}$
;
(4)如果$x= 3x+2$,那么$x-$
3x
$=2$,根据
等式的基本性质1,两边都减去3x
.
答案:
(1)-2y 等式的基本性质2,两边都乘-10
(2)-y 等式的基本性质2,两边都除以-2
(3)6 等式的基本性质2,两边都乘$\frac{3}{2}$
(4)3x 等式的基本性质1,两边都减去3x
13. 利用等式的基本性质,将下面的等式变形为$x= c$的形式:
(1)$2x-2= 5$;
(2)$3= 2x+1$;
(3)$\frac {1}{3}x+3= -6$;
(4)$5x+1= 2x+10$.
答案:
(1)x=$\frac{7}{2}$
(2)x=1
(3)x=-27
(4)x=3)
14. 某同学对$3a-2b= 2a-2b$进行变形,等式两边都加上$2b$,得$3a= 2a$,等式两边都除以$a$,得$3= 2$.你能指出他错在哪里了吗?
答案:解:a是有可能等于0的,当a=0时,等式两边都除以a不符合等式的基本性质.