1. 下列说法正确的是 (
D
)
A.$\frac{-2 x^2 y}{3}$不是单项式,因为有除法运算
B.$3 x^2-\frac{1}{x}$是二次二项式
C.$\frac{x+y}{3}$是单项式
D.整式中不是单项式就是多项式
答案:D
2. 代数式$-4 \pi x y^2$的系数与次数分别是 (
A
)
A.$-4 \pi, 3$
B.$-4 \pi, 4$
C.$-4,3$
D.$-4,4$
答案:A
解析:
代数式$-4\pi xy^2$的系数是$-4\pi$;次数是$1 + 2=3$。
A
3. 在$-4,2 a, \frac{y}{3}, \frac{5}{x}, x-2 y$这些式子中,整式的个数是 (
C
)
A.2
B.3
C.4
D.5
答案:C
解析:
整式有$-4$,$2a$,$\frac{y}{3}$,$x-2y$,共4个。
C
4. (2024·重庆B卷)已知整式$M: a_n x^n+a_{n-1} x^{n-1}+…+a_1 x+a_0$,其中$n, a_{n-1}, …, a_0$为自然数,$a_n$为正整数,且$n+a_n+a_{n-1}+…+a_1+a_0= 5$. 下列说法: (1)满足条件的整式$M$中有5个单项式; (2)不存在任何一个$n$,使得满足条件的整式$M$有且只有3个; (3)满足条件的整式$M$共有16个. 其中正确的个数是 (
D
)
A.0
B.1
C.2
D.3
答案:D
5. 在如图所示的运算程序中,若开始输入$x$的值为5,则第100次输出的结果是 (
C
)
A.8
B.4
C.2
D.1
答案:C
解析:
第1次:输入5(奇数),输出$3×5 + 1 = 16$
第2次:输入16(偶数),输出$\frac{1}{2}×16 = 8$
第3次:输入8(偶数),输出$\frac{1}{2}×8 = 4$
第4次:输入4(偶数),输出$\frac{1}{2}×4 = 2$
第5次:输入2(偶数),输出$\frac{1}{2}×2 = 1$
第6次:输入1(奇数),输出$3×1 + 1 = 4$
第7次:输入4(偶数),输出$\frac{1}{2}×4 = 2$
第8次:输入2(偶数),输出$\frac{1}{2}×2 = 1$
从第3次开始,输出结果以4,2,1循环,周期为3
$(100 - 2)÷3 = 32\cdots\cdots2$,循环中第2个数为2
C
6. (2024·泗阳期末)观察下列各式: $2^2-2 × 1= 1+1,3^2-2 × 2= 4+1,4^2-2 × 3= 9+1,5^2-2 × 4= 16+1, …$, 第$n$个等式是
$(n+1)^{2}-2n=n^{2}+1$
.
答案:$(n+1)^{2}-2n=n^{2}+1$
7. (2024·泗洪期中)多项式$1+2 x y-3 x y^3$的次数为
4
.
答案:4
解析:
多项式的次数是多项式中次数最高的项的次数。在多项式$1 + 2xy - 3xy^3$中,各项的次数依次为:常数项$1$的次数是$0$;$2xy$的次数是$1 + 1 = 2$;$-3xy^3$的次数是$1 + 3 = 4$。所以该多项式的次数为$4$。
4
8. (2024·甘孜)已知$x^2+2 x= 3$,那么$2 x^2+4 x-5$的值是
1
.
答案:1
解析:
因为$x^2 + 2x = 3$,所以$2x^2 + 4x = 2(x^2 + 2x) = 2×3 = 6$,则$2x^2 + 4x - 5 = 6 - 5 = 1$。
1
9. 如图是由火柴棒摆成的图案,按此规律摆放,第⑦个图案中有
15
根火柴棒.
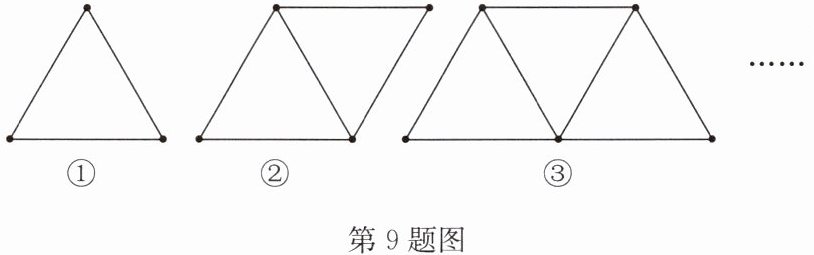
答案:15
解析:
第①个图案火柴棒数量:3
第②个图案火柴棒数量:5
第③个图案火柴棒数量:7
规律:第$n$个图案火柴棒数量为$2n+1$
第⑦个图案:$2×7+1=15$
15