1. 2023年的亚运会在浙江举行,其中金华场馆中心的草坪像“毛毯”,灯光会“跳舞”,实属世界首创,其中草坪内隐藏了近40000个发光点,将数据“40000”用科学记数法表示为 (
B
)
A.$4×10^{5}$
B.$4×10^{4}$
C.$0.4×10^{5}$
D.$0.4×10^{4}$
答案:B
解析:
科学记数法的表示形式为$a×10^{n}$,其中$1\leq\vert a\vert\lt10$,$n$为整数。确定$n$的值时,要看把原数变成$a$时,小数点移动了多少位,$n$的值与小数点移动的位数相同。当原数绝对值$\gt1$时,$n$是正数;当原数绝对值$\lt1$时,$n$是负数。
将$40000$转变为$a×10^{n}$的形式,$a=4$,小数点向左移动了$4$位,所以$n=4$,即$40000=4×10^{4}$。
B
2. (2024·包头)若$m$,$n$互为倒数,且满足$m+mn = 3$,则$n$的值为 (
B
)
A.$\frac{1}{4}$
B.$\frac{1}{2}$
C.2
D.4
答案:B
解析:
因为$m$,$n$互为倒数,所以$mn = 1$。
已知$m + mn = 3$,将$mn = 1$代入得:$m + 1 = 3$,解得$m = 2$。
又因为$mn = 1$,$m = 2$,所以$2n = 1$,解得$n=\frac{1}{2}$。
B
3. (2024·通州期末)计算$(-3)×\frac{1}{3}÷(-\frac{1}{3})×3$的结果是 (
A
)
A.9
B.$-9$
C.1
D.$-1$
答案:【解析】:
本题考查有理数的乘除混合运算,需要按照运算的优先级(先乘除后加减,同级运算从左到右)进行计算。
首先,我们按照运算顺序逐步计算:
$(-3) × \frac{1}{3} = -1$
接着,
$-1 ÷ (-\frac{1}{3}) = -1 × (-3) = 3$
最后,
$3 × 3 = 9$
所以,$(-3) × \frac{1}{3} ÷ (-\frac{1}{3}) × 3 = 9$。
【答案】:
A. $9$
4. (2024·钟吾初中月考)计算$(-\frac{5}{12})^{2025}×(-2\frac{2}{5})^{2025}$的结果为 (
B
)
A.$-1$
B.1
C.0
D.2025
答案:【解析】:
本题主要考查了积的乘方逆运算和有理数的乘法。
首先,我们可以将$(-2\frac{2}{5})$转化为分数形式,即$-\frac{12}{5}$。
然后,我们可以将原式写为$\left(-\frac{5}{12}\right)^{2025} × \left(-\frac{12}{5}\right)^{2025}$。
根据积的乘方逆运算,$a^n × b^n = (a × b)^n$,我们可以将原式进一步化简为:
$\left(-\frac{5}{12} × -\frac{12}{5}\right)^{2025} = 1^{2025} = 1$。
【答案】:B
5. (2024·惠山区期中)有理数$a$,$b$,$c$满足$a + b + c = 0$,且$\vert a\vert\lt\vert b\vert\lt\vert c\vert$,则下列结论正确的是 (
D
)
A.$a = 0$
B.$ab\lt0$
C.$abc\lt0$
D.$\vert a\vert+\vert b\vert=\vert c\vert$
答案:解:
已知$a + b + c = 0$,则$c = - (a + b)$。
由$\vert a\vert\lt\vert b\vert\lt\vert c\vert$,假设$a$、$b$同号,不妨设$a\gt0$,$b\gt0$,则$c = - (a + b)\lt0$,此时$\vert c\vert = a + b = \vert a\vert + \vert b\vert$;同理,若$a\lt0$,$b\lt0$,则$c\gt0$,$\vert c\vert = \vert a\vert + \vert b\vert$。
若$a$、$b$异号,设$a\gt0$,$b\lt0$,且$\vert b\vert\gt\vert a\vert$,则$c = - (a + b) = \vert b\vert - a$,此时$\vert c\vert = \vert b\vert - \vert a\vert$,与$\vert c\vert\gt\vert b\vert$矛盾,故$a$、$b$必同号,$\vert c\vert = \vert a\vert + \vert b\vert$。
A. 若$a = 0$,则$b + c = 0$,$\vert b\vert = \vert c\vert$,与$\vert b\vert\lt\vert c\vert$矛盾,A错误;
B. $a$、$b$同号,$ab\gt0$,B错误;
C. 若$a$、$b$同正,$c$负,$abc\lt0$;若$a$、$b$同负,$c$正,$abc\gt0$,C错误;
D. $\vert a\vert + \vert b\vert = \vert c\vert$,正确。
答案:D
6. (2024·呼和浩特)2023年呼和浩特市政府工作报告中指出,我市主要经济指标增速达到十年来最好水平,地区生产总值完成3802亿元.数据“3802亿”用科学记数法表示为______
$3.802 × 10^{11}$
.
答案:【解析】:
本题考查科学记数法的表示方法。
科学记数法是一种表示大数或小数的方法,其形式为 $a × 10^{n}$,其中 $1 \leq a < 10$ 且 $n$ 为整数。
要将“3802亿”转换为科学记数法,首先明确“亿”是 $10^{8}$。
因此,3802亿等于 $3802 × 10^{8}$。
接下来,将3802转换为科学记数法中的 $a$,即 $3.802$,并相应地调整指数 $n$。
所以,3802亿可以表示为 $3.802 × 10^{11}$。
【答案】:
$3.802 × 10^{11}$
7. (2024·湖滨新区期中)若$\vert a - 1\vert+(b + 2)^{2}= 0$,则$(a + b)^{2025}+a^{2024}= $
0
.
答案:【解析】:
本题主要考查了非负数的性质以及代数式的求值。
由于绝对值和平方都是非负数,且它们的和为0,那么这两个非负数都必须为0。
因此,有:
$\vert a - 1\vert = 0$
$(b + 2)^{2} = 0$
解这两个方程,得到:
$a - 1 = 0 \Rightarrow a = 1$
$b + 2 = 0 \Rightarrow b = -2$
将$a$和$b$的值代入$(a + b)^{2025} + a^{2024}$,得到:
$(1 - 2)^{2025} + 1^{2024} = (-1)^{2025} + 1 = -1 + 1 = 0$
【答案】:
0
8. (2024·六合区期中)已知$a$,$b$互为倒数,$c$,$d$互为相反数,$m$的绝对值是最小的正整数,那么$(-ab)^{2023}-(c + d)^{2024}-m^{2025}$的值为
$-2$或$0$
.
答案:$-2$或$0$。
9. (2024·广陵区期末)在数轴上表示$a$,0,1,$b$四个数的点如图所示,已知点$A到点O的距离等于点B到点O$的距离,则化简$\vert a + b\vert+\vert\frac{a}{b}\vert+\vert a + 1\vert=$
-a
.
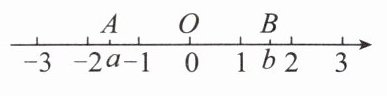
答案:-a
10. (2024·张家港期末)定义新运算“$\diamond$”:对于两个有理数$a$,$b$,$a\diamond b = a^{2}-a(2b + 1)$,例如,$1\diamond2 = 1^{2}-1×(2×2 + 1)= 1 - 5= -4$,那么$(-3)\diamond(-4)= $
-12
.
答案:解:$(-3)\diamond(-4)$
$=(-3)^{2}-(-3)×[2×(-4)+1]$
$=9 - (-3)×(-8 + 1)$
$=9 - (-3)×(-7)$
$=9 - 21$
$=-12$
$-12$
11. (30分)计算:
(1)$(-1\frac{1}{2})^{3}÷(-\frac{3}{4})^{3}$;
(2)$-2^{3}÷\frac{4}{9}×(-\frac{2}{3})^{2}$;
(3)$12÷(-3)-(-8)×(-\frac{3}{4})×\frac{1}{2}$;
(4)$(-0.25)^{3}×(-4)^{2}÷(-1)^{2025}$;
(5)$(\frac{2}{3}-\frac{1}{10}+\frac{1}{6}-\frac{2}{5})÷(-\frac{1}{30})$;
(6)$[(-72)×(-\frac{2}{3})]×[(-\frac{3}{5})÷(-\frac{8}{15})]$.
答案:(1)解:原式$=(-\frac{3}{2})^{3}÷(-\frac{3}{4})^{3}$
$=(-\frac{27}{8})÷(-\frac{27}{64})$
$=(-\frac{27}{8})×(-\frac{64}{27})$
$=8$
(2)解:原式$=-8÷\frac{4}{9}×\frac{4}{9}$
$=-8×\frac{9}{4}×\frac{4}{9}$
$=-8$
(3)解:原式$=-4 - 8×\frac{3}{4}×\frac{1}{2}$
$=-4 - 3$
$=-7$
(4)解:原式$=(-\frac{1}{4})^{3}×16÷(-1)$
$=(-\frac{1}{64})×16×(-1)$
$=\frac{1}{4}$
(5)解:原式$=(\frac{2}{3}-\frac{1}{10}+\frac{1}{6}-\frac{2}{5})×(-30)$
$=\frac{2}{3}×(-30)-\frac{1}{10}×(-30)+\frac{1}{6}×(-30)-\frac{2}{5}×(-30)$
$=-20 + 3 - 5 + 12$
$=-10$
(6)解:原式$=48×(\frac{3}{5}×\frac{15}{8})$
$=48×\frac{9}{8}$
$=54$