9.如图所示的四个图形是多面体的展开图,请你在各个展开图下面的横线上写上相应几何体的名称.
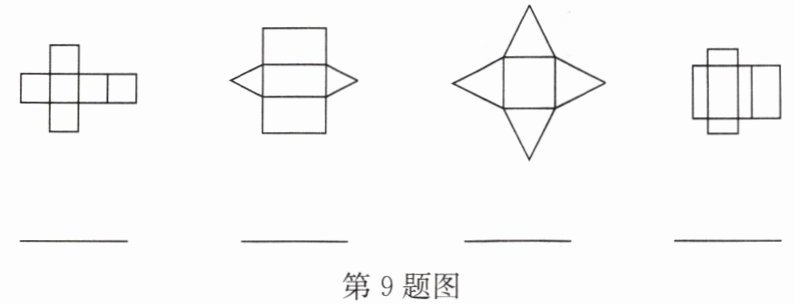
正方体
三棱柱
四棱锥
长方体
答案:正方体 三棱柱 四棱锥 长方体
10.我国宋朝时期的数学家杨辉,曾将大小完全相同的圆柱形木桩逐层堆积,形成“三角垛”,顶层记为第1层,有1根圆木桩;前2层有3根圆木桩;前3层有6根圆木桩,往下依次是前4层,前5层,…,如图给出了前4层.若用$a_n表示前n$层的圆木桩数目,其中$n = 1,2,3,…$,则$\frac{1}{a_1} + \frac{1}{a_2} + \frac{1}{a_3} + … + \frac{1}{a_{16}}$的值是______
$\frac{32}{17}$
.

答案:$\frac{32}{17}$
解析:
由题意得,$a_1=1$,$a_2=3=1+2$,$a_3=6=1+2+3$,$a_4=10=1+2+3+4$,
则$a_n=1+2+3+\cdots+n=\frac{n(n+1)}{2}$,
所以$\frac{1}{a_n}=\frac{2}{n(n+1)}=2\left(\frac{1}{n}-\frac{1}{n+1}\right)$,
$\frac{1}{a_1}+\frac{1}{a_2}+\cdots+\frac{1}{a_{16}}=2\left[\left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\cdots+\left(\frac{1}{16}-\frac{1}{17}\right)\right]$
$=2\left(1-\frac{1}{17}\right)=2×\frac{16}{17}=\frac{32}{17}$
$\frac{32}{17}$
11.(14分)一个直棱柱有18个面,且所有的侧棱长的和为64cm,底面边长都是3cm.
(1)这是几棱柱?
(2)求此棱柱的侧面积.
答案:
(1)十六棱柱.
(2)由题意得,侧棱长为$64÷16=4(\text{cm})$,$4×3×16=192(\text{cm}^2)$,即此棱柱的侧面积是$192\ \text{cm}^2$.
12.(16分)如图是一个长方体的表面展开图.
(1)折叠成长方体后,与字母N重合的点是
H,J
;
(2)若$AG = CK = 14cm$,$FG = 2cm$,求该长方体的表面积和体积.

(2)解:由$AG=CK=14\ \text{cm}$,$FG=2\ \text{cm}$,可得$BC=LK=5\ \text{cm}$,$CL=CK-LK=14-5=9(\text{cm})$,长方体的表面积为$2×(9×5+2×5+2×9)=146(\text{cm}^2)$,体积为$5×9×2=90(\text{cm}^3)$.答:该长方体的表面积为$146\ \text{cm}^2$,体积为$90\ \text{cm}^3$.
答案:
(1)H,J
(2)解:由$AG=CK=14\ \text{cm}$,$FG=2\ \text{cm}$,可得$BC=LK=5\ \text{cm}$,$CL=CK-LK=14-5=9(\text{cm})$,长方体的表面积为$2×(9×5+2×5+2×9)=146(\text{cm}^2)$,体积为$5×9×2=90(\text{cm}^3)$.答:该长方体的表面积为$146\ \text{cm}^2$,体积为$90\ \text{cm}^3$.
13.(20分)数学课上,老师让同学们用若干个正方形和长方形拼成一个长方体的展开图.拼完后,小明看来看去觉得所拼图形(如图)似乎存在问题.
(1)请你帮小明分析一下拼图是否存在问题,若有多余块,则把图中多余块涂黑;若还缺少,则直接在原图中补全.
(2)长方体共有______条棱,若将一个长方体沿某些棱剪开展成(1)中修正后的平面图形,需要剪开______条棱.
(3)根据图中的数据,求出由修正后的展开图折叠成的长方体的体积.

答案:(1)解:有多余块,如答图.

(2)12 7
(3)解:底面正方形的边长为$12÷4=3(\text{cm})$,长方体的高为$17-3×3=8(\text{cm})$,长方体的体积为$3×3×8=72(\text{cm}^3)$.答:由修正后的展开图折叠成的长方体的体积为$72\ \text{cm}^3$.