1. 两边和它们的夹角
分别相等
的两个三角形全等(可以简写成
边角边
或
SAS
).
答案:分别相等 边角边 SAS
如图,在$\triangle ABC和\triangle DEF$中,
$\left\{\begin{array}{l} AB=
DE
, \\
∠B
=
∠E
, \\
BC
= EF, \end{array} \right.$
$\therefore \triangle ABC\cong \triangle DEF(
SAS
)$
答案:DE ∠B ∠E BC SAS
解析:
在$\triangle ABC$和$\triangle DEF$中,
$\left\{\begin{array}{l} AB=DE, \\ ∠B=∠E, \\ BC=EF, \end{array} \right.$
$\therefore \triangle ABC\cong \triangle DEF(SAS)$
1. 如图,点$B,F,C,E$在同一条直线上,$AB= DE,BF= CE,AB// DE$,求证:$AC= DF$.
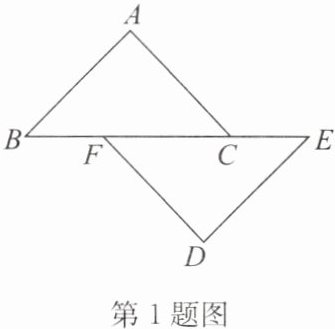
答案:证明:∵AB//DE,∴∠B=∠E.
∵BF=CE,∴BF+FC=CE+FC,即 BC=EF.
又 AB=DE,∴△ABC≌△DEF(SAS).∴AC=DF.
2. 如图,$AB= AD,AC= AE,∠BAE= ∠DAC$. 求证:$∠C= ∠E$.

答案:证明:∵∠BAE=∠DAC,
∴∠BAE+∠CAE=∠DAC+∠CAE,
即∠CAB=∠EAD,又 AB=AD,AC=AE,
∴△ABC≌△ADE(SAS),∴∠C=∠E.
3. (2024春·成都期末)某数学兴趣小组的同学测量一个小口圆形容器内径时遇到了困难,小组同学们借用学过的三角形全等的知识合作制作了特制工具测量器. 如图所示,将等长的钢条$AD和BC的中点O$焊接在一起,制作了一把“X”形卡钳. 根据“X”形卡钳的制作原理能判断$\triangle ABO\cong \triangle DCO$,从而测量出$AB$的长,就等于内径$CD$的长. 请写出$\triangle ABO\cong \triangle DCO$的理由.

答案:解:在△AOB 和△DOC 中,
OA=OD,
∠AOB=∠DOC,
BO=CO,
∴△AOB≌△DOC(SAS).