分式的基本性质:
分式的分子与分母乘(或除以)同一个不等于0的整式,分式的值不变
.
答案:分式的分子与分母乘(或除以)同一个不等于0的整式,分式的值不变
1.(2024 春·工业园区期末)下列式子从左到右变形一定正确的是 (
D
)
A.$\frac {a}{b}= \frac {a^{2}}{b^{2}}$
B.$\frac {a}{b}= \frac {a+1}{b+1}$
C.$\frac {a}{b}= \frac {a-1}{b-1}$
D.$\frac {a^{2}}{ab}= \frac {a}{b}$
答案:D
解析:
解:A. 当$a=1$,$b=2$时,$\frac{a}{b}=\frac{1}{2}$,$\frac{a^2}{b^2}=\frac{1}{4}$,$\frac{1}{2}\neq\frac{1}{4}$,故A错误;
B. 当$a=1$,$b=2$时,$\frac{a}{b}=\frac{1}{2}$,$\frac{a+1}{b+1}=\frac{2}{3}$,$\frac{1}{2}\neq\frac{2}{3}$,故B错误;
C. 当$a=2$,$b=3$时,$\frac{a}{b}=\frac{2}{3}$,$\frac{a-1}{b-1}=\frac{1}{2}$,$\frac{2}{3}\neq\frac{1}{2}$,故C错误;
D. $\frac{a^2}{ab}$的分子分母同时除以$a$($a\neq0$),可得$\frac{a}{b}$,故D正确。
答案:D
2.下列各式正确的是 (
C
)
A.$\frac {2ab}{4a^{2}c}= \frac {b}{2c}$
B.$\frac {a+b}{ab}= \frac {1+b}{b}$
C.$\frac {x-3}{x^{2}-9}= \frac {1}{x+3}$
D.$\frac {-x+y}{2}= -\frac {x+y}{2}$
答案:C
解析:
解:
A. $\frac{2ab}{4a^2c}=\frac{b}{2ac}$,原选项错误。
B. $\frac{a+b}{ab}=\frac{1}{b}+\frac{1}{a}$,原选项错误。
C. $\frac{x-3}{x^2-9}=\frac{x-3}{(x+3)(x-3)}=\frac{1}{x+3}$($x\neq3$),正确。
D. $\frac{-x+y}{2}=-\frac{x-y}{2}$,原选项错误。
答案:C
3.将分式$\frac {xy}{2x+y}$中的x,y的值都变为原来的2倍,则该分式的值 (
A
)
A.变为原来的2倍
B.变为原来的4倍
C.不变
D.变为原来的一半
答案:A
解析:
解:将x,y的值都变为原来的2倍,新分式为$\frac{(2x)(2y)}{2(2x)+(2y)}=\frac{4xy}{4x+2y}=\frac{4xy}{2(2x+y)}=\frac{2xy}{2x+y}$。原分式为$\frac{xy}{2x+y}$,新分式是原分式的2倍。
答案:A
4.若$\frac {2(x-1)}{3(x-1)}= \frac {2}{3}$成立,则x的取值范围是
x≠1
.
答案:x≠1
解析:
要使等式$\frac {2(x - 1)}{3(x - 1)}=\frac {2}{3}$成立,分母不能为$0$,即$3(x - 1)\neq0$,解得$x\neq1$。
故答案为:$x\neq1$
5.在括号内填上使等式成立的分子或分母.
(1)$\frac {x}{3y}= \frac {
2x²y
}{6xy^{2}}$;
(2)$\frac {2x^{2}y}{xy^{3}}= \frac {
2x
}{y^{2}}$;
(3)$\frac {-2x}{1-2x}= \frac {
2x²
}{2x^{2}-x}$;
(4)$\frac {x-y}{5y}= \frac {(y-x)^{2}}{
5xy-5y²
}$.
答案:(1)2x²y (2)2x (3)2x² (4)5xy-5y²
解析:
(1) 观察等式左边分母为$3y$,右边分母为$6xy^{2}$,右边分母是左边分母乘$2xy$,根据分式基本性质,分子也要乘$2xy$,$x×2xy = 2x^{2}y$,故括号内填$2x^{2}y$。
(2) 左边分子分母同时约去$xy$($x\neq0$,$y\neq0$),$\frac{2x^{2}y}{xy^{3}}=\frac{2x}{y^{2}}$,所以括号内填$2x$。
(3) 右边分母$2x^{2}-x = x(2x - 1)=-x(1 - 2x)$,左边分母是$1 - 2x$,右边分母是左边分母乘$-x$,分子也要乘$-x$,$-2x×(-x)=2x^{2}$,故括号内填$2x^{2}$。
(4) 分子$(y - x)^{2}=(x - y)^{2}$,左边分子是$x - y$,右边分子是左边分子乘$(x - y)$,分母也要乘$(x - y)$,$5y(x - y)=5xy - 5y^{2}$,故括号内填$5xy - 5y^{2}$。
答案:(1)$2x^{2}y$;(2)$2x$;(3)$2x^{2}$;(4)$5xy - 5y^{2}$
6.不改变分式的值,使下列分式的分子和分母都不含“一”:
(1)$\frac {-5y}{-x^{2}}$;
(2)$\frac {-a}{2b}$;
(3)$\frac {4m}{-3n}$;
(4)$-\frac {-x}{2y}$.
答案:解:(1)$\frac{5y}{x^2}$.(2)$-\frac{a}{2b}$.(3)$-\frac{4m}{3n}$.(4)$\frac{x}{2y}$.
7.不改变分式的值,使下列各分式的分子、分母的最高次项的系数都是正数.
(1)$\frac {2-a}{a^{2}-4}$;
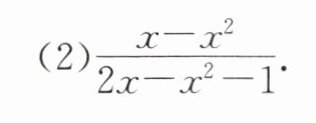
答案:解:(1)$\frac{2-a}{a^2-4}=-\frac{a-2}{a^2-4}$.(2)$\frac{x-x^2}{2x-x^2-1}=-\frac{x^2-x}{x^2-2x+1}$.
解析:
解:(2)$\frac{x - x^2}{2x - x^2 - 1}=-\frac{x^2 - x}{x^2 - 2x + 1}$
8.不改变分式的值,把下列各分式的分子与分母中的各项系数都化为整数.
(1)$\frac {0.5x-0.2y}{0.3x+2y}$;
(2)$\frac {a+\frac {1}{4}b}{\frac {4}{3}a-2b}$.
答案:解:(1)原式=$\frac{10×(0.5x-0.2y)}{10×(0.3x+2y)}=\frac{5x-2y}{3x+20y}$.(2)原式=$\frac{12×\left(a+\frac{1}{4}b\right)}{12×\left(\frac{4}{3}a-2b\right)}=\frac{12a+3b}{16a-24b}$.