如果一个三角形有两个角相等,那么
这两个角所对的边也相等
.
答案:这两个角所对的边也相等
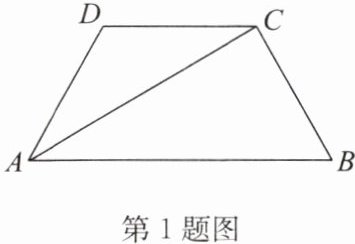
1.(2024春·宿豫区期末)如图,已知AB//CD,AC平分∠DAB.求证:△ADC是等腰三角形.
答案:证明:∵AB//CD,∴∠BAC=∠DCA.
∵AC平分∠DAB,∴∠BAC=∠DAC.
∴∠DAC=∠DCA,∴△ADC是等腰三角形.
2.如图,BD,CE是△ABC的高,且BD= CE.求证:△ABC是等腰三角形.

答案:证明:∵BD,CE是△ABC的高,
∴∠CEB=∠BDC=90°.
在Rt△BCE和Rt△CBD中,
BC=CB,
CE=BD,
∴Rt△BCE≌Rt△CBD(HL),
∴∠ABC=∠ACB,∴△ABC是等腰三角形.
3.如图,在△ABC中,AD平分∠BAC,BD= CD,DE⊥AB于点E,DF⊥AC于点F.求证:AB= AC.

答案:证明:∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
根据角平分线上的点到角两边的距离相等得出DE=DF,
又∵BD=CD,∠DEB=∠DFC=90°,
∴Rt△DEB≌Rt△DFC(HL),∴∠B=∠C,∴AB=AC.
4.如图,在△ABC中,E为AB上一点,连接CE,EC= BC,过点C作CD= AC,且∠1= ∠2,连接DE.若∠B= 75°,求∠3的度数.

答案:解:∵∠1=∠2,
∴∠1+∠ACE=∠2+∠ACE,
∴∠DCE=∠ACB,
在△DCE和△ACB中,CD=AC,
∠DCE=∠ACB,
EC=BC,
∴△DCE≌△ACB(SAS),
∴∠DEC=∠B=75°.
∵EC=BC,
∴∠CEB=∠B=75°,
∴∠DEB=∠DEC+∠CEB=150°,
∴∠3=180°-∠DEB=30°.