1. 线段的垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等
.
答案:线段垂直平分线上的点与这条线段两个端点的距离相等
2. 线段的垂直平分线的判定:
与线段两个端点距离相等的点在这条线段的垂直平分线上
.
答案:与线段两个端点距离相等的点在这条线段的垂直平分线上
∵ 直线 $ l $ 垂直平分 $ AB $,
∴
PA
$ = $
PB
.
判定:
∵
PA
$ = $
PB
,
∴ 点 $ P $ 在 $ AB $ 的垂直平分线上.
答案:PA PB PA PB
解析:
性质:∵ 直线 $ l $ 垂直平分 $ AB $,
∴ $ PA = PB $.
判定:∵ $ PA = PB $,
∴ 点 $ P $ 在 $ AB $ 的垂直平分线上.
1. 点 $ P $ 到 $ \triangle ABC $ 的三个顶点的距离相等,则点 $ P $ 是 $ \triangle ABC $ ______ 的交点 (
C
)
A.三条高
B.三条角平分线
C.三边的垂直平分线
D.三条中线
答案:C
解析:
点P到△ABC的三个顶点的距离相等,根据线段垂直平分线上的点到线段两端距离相等的性质,可知点P在△ABC三边的垂直平分线上。因此,点P是△ABC三边的垂直平分线的交点。
C
2. 如图,$ BA $ 平分 $ \angle CBD $,$ AB $ 平分 $ \angle CAD $. 求证:$ AB $ 垂直平分 $ CD $.
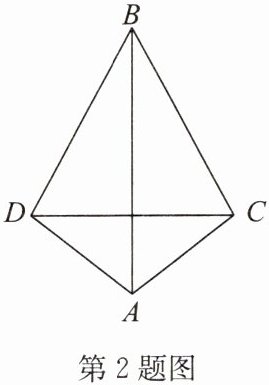
答案:证明:∵BA平分∠CBD,∴∠DBA=∠CBA.
∵AB平分∠CAD,∴∠DAB=∠CAB.
在△BAD和△BAC中,∠DBA=∠CBA, BA=BA, ∠DAB=∠CAB,
∴△BAD≌△BAC(ASA),
∴DB=CB,AD=AC,
∴点B,A都在DC的垂直平分线上,
∴AB垂直平分CD.
3. 如图,$ \text{Rt} \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ D $ 是 $ AB $ 上一点,$ BD = BC $,过点 $ D $ 作 $ AB $ 的垂线交 $ AC $ 于点 $ E $,连接 $ BE $,$ CD $. 求证:$ BE $ 垂直平分 $ CD $.

答案:证明:∵∠ACB=90°,DE⊥AB,
∴∠ACB=∠BDE=90°.
在Rt△BDE和Rt△BCE中, BE=BE, BD=BC,
∴Rt△BDE≌Rt△BCE,∴ED=EC.
∵ED=EC,BD=BC,∴BE垂直平分CD.