1. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = BC$,$D为CB$的延长线上一点,$AE = AD$,延长$AC交BE于点P$,且$BP = PE$。若$\frac{BD}{BC} = \frac{2}{3}$,则$\frac{AC}{PC}$的值为
3
。
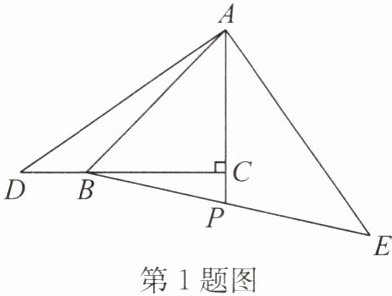
答案:3 点拨:过点E作EF⊥AP交AP的延长线于点F,则△BCP≌△EFP,∴EF=BC=AC.∵AE=AD,
∴Rt△AEF≌Rt△DAC(HL),∴∠EAP=∠ADC,AF=DC;∵∠ADC+∠DAC=90°,∴∠EAP+∠DAC=90°,
即∠DAE=90°,∴AE⊥AD.
令k>0,设BD=2k,BC=3k,则AF=DC=5k,AC=3k,∴CP=PF=k,∴$\frac{AC}{PC}$=3.
2. 如图,$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$D是AC$边上一点,$CD = CB$,过点$B作BE \perp AB且BE = AB$,连接$DE交BC的延长线于点F$,求证:$DF = EF$。

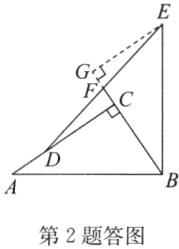
答案:证明:过点E作EG⊥BF,交BF的延长线于点G,如答图,∵EG⊥BF,∴∠EGF=90°,∴∠GBE+∠BEG=90°.∵BE⊥AB,∴∠ABE=90°=∠ABC+∠EBC,
∴∠ABC=∠BEG.
在△ABC和△BEG中,$\left\{\begin{array}{l} ∠ACB=∠BGE=90^{\circ },\\ ∠ABC=∠BEG,\\ AB=BE,\end{array}\right. $
∴△ABC≌△BEG(AAS),∴EG=BC;
∵CD=BC,∴EG=CD.
在△EGF和△DCF中,$\left\{\begin{array}{l} ∠EGF=∠DCF=90^{\circ },\\ ∠EFG=∠DFC,\\ EG=DC,\end{array}\right. $
∴△EGF≌△DCF(AAS),∴EF=DF.
3. (2024春·驻马店月考)如图,在四边形$ABCD$中,$AD // BC$,$E为CD$的中点,连接$AE$,$BE$,延长$AE交BC的延长线于点F$。
(1)$\triangle DAE和\triangle CFE$全等吗?说明理由;
(2)若$AB = BC + AD$,求证:$BE \perp AF$;
(3)在(2)的条件下,若$EF = 6$,$CE = 5$,$\angle D = 90^{\circ}$,求点$E到AB$的距离。

答案:(1)解:△DAE≌△CFE;理由如下:
∵AD//BC,∴∠ADC=∠ECF.
∵E是CD的中点,∴DE=EC.
在△ADE和△FCE中,$\left\{\begin{array}{l} ∠ADE=∠FCE,\\ DE=EC,\\ ∠AED=∠FEC,\end{array}\right. $
∴△ADE≌△FCE(ASA).
(2)证明:∵△ADE≌△FCE,∴AE=EF,AD=CF.∵AB=BC+AD,∴AB=BC+CF,即AB=BF.
在△ABE和△FBE中,$\left\{\begin{array}{l} AB=FB,\\ AE=FE,\\ BE=BE,\end{array}\right. $
∴△ABE≌△FBE(SSS),
∴∠AEB=∠FEB=90°,∴BE⊥AE.
(3)解:在(2)的条件下有△ABE≌△FBE,
∴∠ABE=∠FBE;
∴点E到BF的距离等于点E到AB的距离,
∵CE⊥BF,CE=5,∴点E到AB的距离为5.