3. 聪聪对下面的问题进行了深入的研究,他的研究过程如下:
【问题再现】
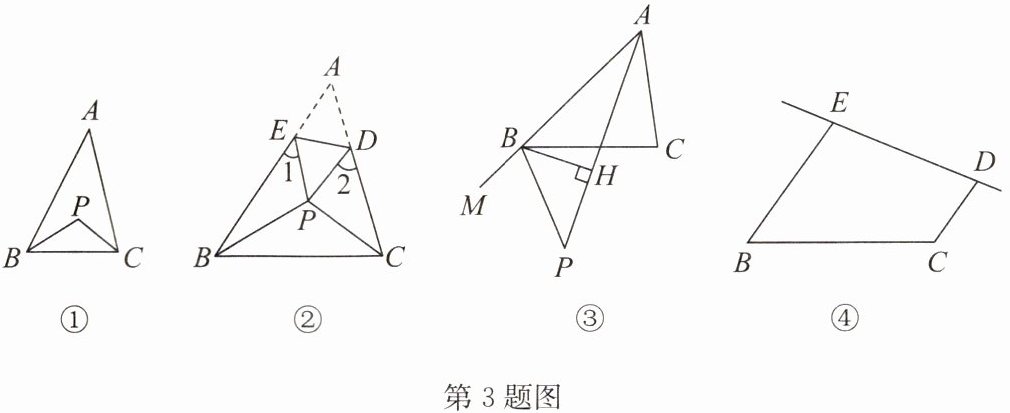
(1)如图①,在$△ABC$中,$∠ABC,∠ACB$的平分线交于点P,$∠A= 40^{\circ }$,则$∠BPC$的度数是____;
【问题解决】
(2)如图②,在$△ABC$中,$∠ABC,∠ACB$的平分线交于点P,将$△ABC$沿DE折叠使得点A与点P重合,若$∠1+∠2= 100^{\circ }$,求$∠BPC$的度数;
【问题推广】
(3)如图③,在$△ABC$中,$∠BAC的平分线与△ABC的外角∠CBM$的平分线交于点P,过点B作$BH⊥AP$于点H,若$∠ACB= 82^{\circ }$,求$∠PBH$的度数;
【拓展提升】
(4)如图④,在四边形BCDE中,$EB// CD$,点F在射线DE上运动(点F不与E,D两点重合),连接BF,CF,$∠EBF,∠DCF$的平分线交于点Q,若$∠EBF= α,∠DCF= β$,直接写出$∠Q$和α,β之间的数量关系.
答案:3.(1)110° 点拨:∵∠A=40°,
∴∠ABC+∠ACB=180°−∠A=140°.
∵BP平分∠ABC,CP平分∠ACB,
∴∠ABC=2∠PBC,∠ACB=2∠PCB,
∴2∠PBC+2∠PCB=140°,即∠PBC+∠PCB=70°,
∴∠P=180°−∠PBC−∠PCB=110°.
(2)解:由折叠的性质可得∠AED=∠PED,∠ADE=∠PDE;
∵∠1+∠AEP=180°,∠2+∠ADP=180°,∠1+∠2=100°,∴2∠AED+2∠ADE=260°,
∴∠AED+∠ADE=130°,
∴∠A=180°−∠AED−∠ADE=50°,
∵∠A=50°,
∴∠ABC+∠ACB=180°−∠A=130°.
∵BP平分∠ABC,CP平分∠ACB,
∴∠ABC=2∠PBC,∠ACB=2∠PCB,
∴2∠PBC+2∠PCB=130°,即∠PBC+∠PCB=65°,
∴∠BPC=180°−∠PBC−∠PCB=115°.
(3)解:∵AP平分∠BAC,BP平分∠CBM,
∴∠BAC=2∠BAP,∠CBM=2∠CBP.
∵∠CBM=∠BAC+∠ACB,
∴∠CBP=∠BAP+41°,
∵∠ABC=180°−∠ACB−∠BAC,
∴∠ABC=98°−2∠BAP.
∵∠ABC+∠CBP+∠BAP+∠P=180°,
∴∠P=180°−∠BAP−∠ABC−∠CBP=41°.
∵BH⊥AP,∴∠BHP=90°,
∴∠PBH=180°−∠P−∠BHP=49°.
(4)解:当点F在点E的左侧时,如答图①所示.
∵EB//CD,∴∠CBE+∠BCD=180°.
∵BQ平分∠EBF,CQ平分∠DCF,
∴∠EBQ=$\frac{1}{2}$∠EBF=$\frac{\alpha}{2}$,∠QCF=$\frac{1}{2}$∠DCF=$\frac{\beta}{2}$,
∴∠Q=180°−∠QBC−∠QCB=180°−∠QBE−∠EBC−∠FCB−∠QCF=$\frac{\beta - \alpha}{2}$.

当点F在D,E两点之间时,如答图②所示.
同理,可得∠FBQ=$\frac{1}{2}$∠EBF=$\frac{\alpha}{2}$,∠QCF=$\frac{1}{2}$∠DCF =$\frac{\beta}{2}$,
∠FBC+∠FCB=180°−∠DCF−∠EBF=180°−α−β,
∴∠Q=180°−∠QBC−∠QCB=180°−∠QBF−∠FBC−∠FCB−∠QCF=$\frac{\alpha + \beta}{2}$.
综上所述,∠Q=$\frac{\alpha + \beta}{2}$或∠Q=$\frac{\beta - \alpha}{2}$.